11 примеров внутренних сил: исчерпывающая информация —
Внутренняя сила противостоит влиянию внешней силы на объект.
Внутренняя сила — это контактная сила, отвечающая за сохранение объекта в неприкосновенности, когда на него действуют нагрузки из-за внешней силы. Он может вызывать ускорение в различных частях, не нарушая равновесия, поскольку действует изнутри объекта.
Нет сила по своей сути является внутренним или внешним; все зависит от того, как учитывать систему и действующие на нее силы. В любой системе с парой действие-противодействие приложенную силу обычно называют внутренней силой. Давайте обсудим список примеров внутренних сил ниже, чтобы понять их физику.
Дрожание дерева от ветраКогда ветер дует на дерево, оно раскачивается.
На эту силу ветра влияют внешние факторы, и дерево может сильно дрожать на своем месте, тем самым вырывая его из земли. С другой стороны, внутренняя сила — это сила, которая помогает дереву оставаться на месте и предотвращает его падение.
Мышечная нагрузка, приложенная к краям измерительной шкалы, может вызвать ее растяжение.
Значительное количество обоих напряжение и сжатие присутствует в измерительной шкале. Внешняя сила — это сила мышц, действующая на весы. Эта сила имеет достаточно большую величину, чтобы согнуть, но не разрушить весы. Это потому, что он поддерживается внутренней силой, которая не дает ему сломаться.
Толкаем автобусТолкание автобуса, сидя внутри и снаружи, приводит к двум различным ситуациям.
Толкание автобуса, сидя внутри, не вызовет никаких движение в этом. В то время как попытка его внешнего использования после выхода из автобуса может заставить его двигаться вперед, потому что внешнее толкание пассажиров создает внешнюю силу на автобусе.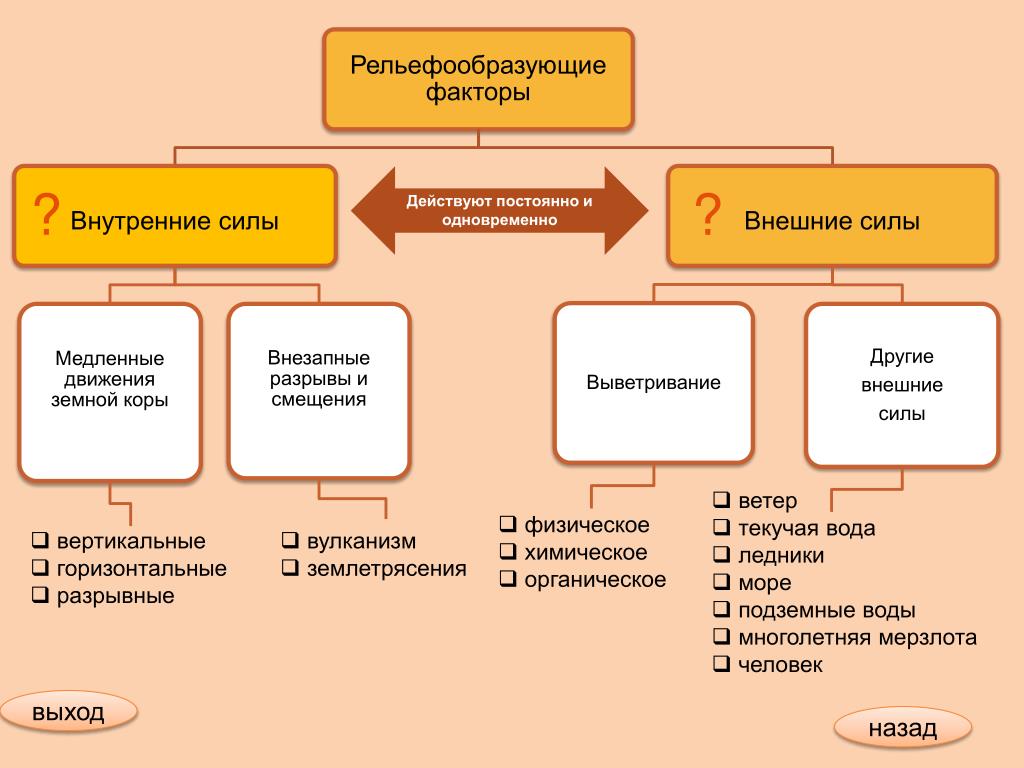
Когда пассажиры сидят внутри автобуса, они образуют совокупную систему, и, следовательно, любая сила, приложенная в это время, не вызывает движения в транспортном средстве. Следовательно, это внутренняя сила, которая существует в системе, которая препятствует ее перемещению и противодействует нагрузке, приложенной внешней силой.
Действие пружиныКогда к пружине прикладывается усилие для ее растяжения, пружина перемещается.
Сила, действующая на пружину, является внешней, тогда как внутренняя сила сжимает пружину, чтобы вернуть ее первоначальную форму. Внутренняя сила диаметрально противоположна внешней силе и противостоит движению и любому изменению формы.
Примеры внутренних сил: действие пружины; Источник изображения: “Натяжные пружины”(CC BY-NC-ND 2.0) от ВольпинТолкание стула
Если толкать стул, сидя на нем и стоя на земле, возникают два разных сценария, которые могут классифицировать внутренние и внешние силы соответственно.
Стул движется в направлении приложенной силы, когда его толкает стоящий рядом человек. В то же время, когда стул толкают, сидя на нем, не наблюдается никакого движения. Обе ситуации демонстрируют одинаковое количество силы, приложенной в одном и том же направлении. Единственное различие заключается в методе оценки.
Первый случай связан с приложением внешней силы, и, следовательно, видно движение в кресле. Однако во второй ситуации стул не двигается, поскольку сидящий на нем человек стал компонентом системы. В результате действующая здесь сила называется внутренней силой.
Сжатие губкиСжатие, действующее на губчатое тело, является еще одним примером. внутренней силы.
Когда человек трется рукой о поверхность губки, форма губки меняется. Поскольку сила человека действует внутри системы, сила сжатия является внутренней силой. Эта внутренняя сила сжатия препятствует движению, которое помогает губке восстановить свою прежнюю форму.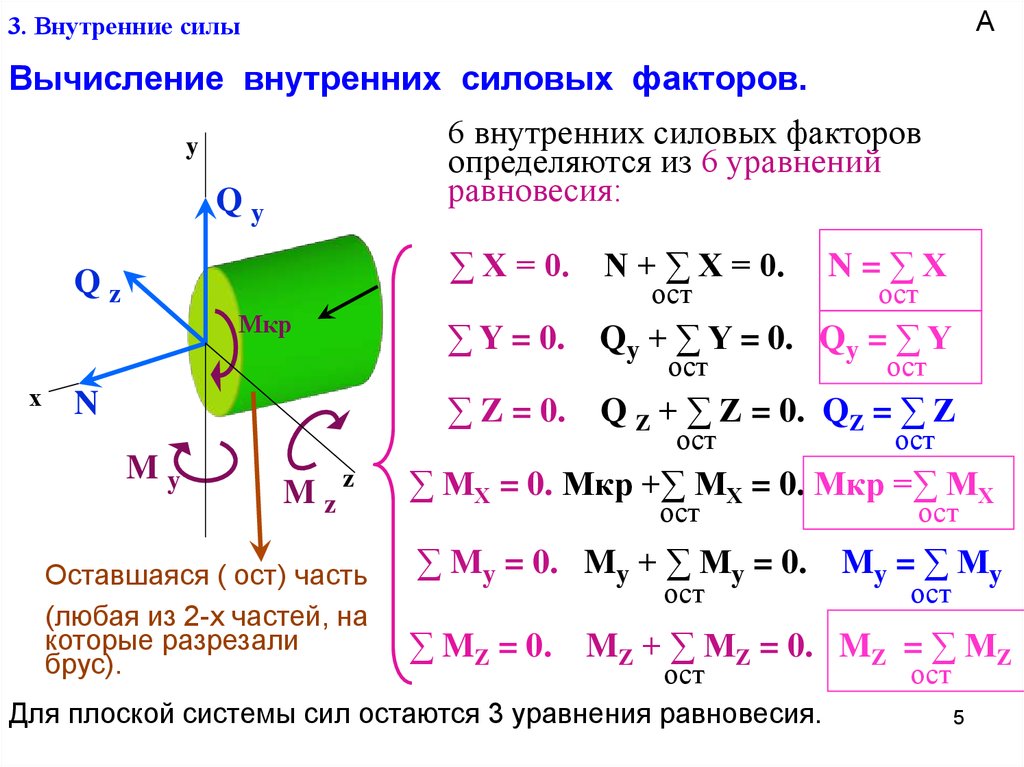
Растяжение резиновой ленты вызывает в ней напряжение, которое является внутренней силой.
Когда резиновую ленту тянут или растягивают, создается сила натяжения. Первоначальная форма объекта восстанавливается при снятии тягового усилия. Сила считается внутренней, потому что взаимодействие происходит внутри объекта или системы. С другой стороны, внешняя сила — это сила, используемая для растягивания ленты и создания движения для изменения ее формы.
Выжимание мочалкиЗакручивающая сила кручения используется для отжима влажной мочалки.
Мочалку скручивают в противоположных направлениях с обоих концов, чтобы выжать из нее воду. Кручение — это сила, которая скручивается или поворачивается и исходит изнутри объекта. Следовательно, это внутренняя сила.
Примеры внутренних сил: отжимание мочалки; Источник изображения: МакспиксельСтолкновение хоккейных шайбРассмотрим две хоккейные шайбы, скользящие по поверхность без трения и сталкивающиеся друг с другом при t=0; чтобы задача была достаточно простой для оценки, мы игнорируем сопротивление воздуха.
Есть три фундаментальные силы работа с телами — сила, действующая взаимно перпендикулярно льду и хоккейным шайбам, сила тяжести и причина трения из-за столкновений между шайбами. Наша система учитывает две шайбы только потому, что наш объект представляет собой движение только между шайбами.
Следовательно, сила трения между шайбами действует как внутренняя сила, потому что сохранение импульса применим в данном случае. Когда остальные Земля входит в нашу систему, гравитация и нормальные силы также становятся внутренними силами.
Кинематика мышц и сухожилий человеческого телаМышцы и сухожилия — это структуры, которые создают силы, вызывающие изменение нашего кинематического состояния.
Мышечная активность генерирует внутренние силы, которые вызывают движения конечностей и других компонентов тела. Тем не менее, невозможно изменить движение центра тяжести человеческого тела без наличия внешних сил. Только когда человеческое тело соприкасается с другим предметом, оно может изменить свое движение.
Исследование внутренней силы может быть использовано для характеристики движений отдельных компонентов тела, а также характера и причин травм.
Землетрясения и извержения вулкановПоверхность Земли, на которой живут люди, характеризуется бесконечным разнообразием морфологических форм.
Узкие канавы спускаются по самой нижней поверхности океана, в то время как огромные бездонные равнины обрывают его до подводных гор и хребтов. В то время как от горных поясов до вулканических цепей и от холмистых областей до плоских низменностей простираются по периферии континентов. Выделение тепла внутри Земли, которое вызывает внутренние или эндогенные силы в геологии.
Внутренние силы ответственны за все вертикальные и горизонтальные движения земной коры, а также за некоторые экстремальные бедствия, такие как землетрясения и извержения вулканов.
Примеры внутренних сил: извержения вулканов; Источник изображения: Темные изображения08, Извержение вулкана Майон 4, CC BY-SA 4. 0Часто задаваемые вопросы (FAQ)В: Чем вызваны внутренние силы?
0Часто задаваемые вопросы (FAQ)В: Чем вызваны внутренние силы?A: Одна часть объекта, воздействуя на другие его части, вызывает внутренние силы.
Внутренняя сила — это совокупность контактных сил, которая не нарушает баланс объекта. Элементы вектора внутренней силы компенсируются и, следовательно, не влияют на конечную силу, приложенную к объекту.
В: Всегда ли внутренние силы уравновешены?A: Внутренние силы обычно называют консервативными, поскольку они не изменяют общую механическую энергию объекта; следовательно, они всегда уравновешиваются в случае недеформируемых твердых тел.
В: Каковы четыре основных типа внутренней силы?A: Четыре основных типа внутренней силы:
- Сжатие: материал сжимается под действием силы «толчка».
- Напряжение: материал изгибается под действием силы натяжения.

- Кручение: материал испытывает скручивающую силу, т. Е. Крутящую силу.
- Изгиб: материал теряет прямолинейность и изгибается.
Внутренние силы
Внутренние силы – это силы междуатомных связей в кристаллической решетке. До деформации силы взаимного притяжения и отталкивания между атомами уравновешены. Под действием внешней силы расстояния между атомами изменяются, одновременно изменяется соотношение между силами притяжения и отталкивания, появляется внутренняя сила, уравновешивающая внешнюю. Внутренние силы, приходящиеся на единицу площади, называют напряжением и обозначают буквой S.
Напряжение равно:
,Н/мм2,
где P– равнодействующая внутренних сил;
F– площадь выделенного внутри тела поперечного сечения, на которую действует силаP.
В
приведенной формуле предполагается
равномерное распределение напряжения
по сечению, т. е. в любой точке сечения
они одинаковы и в этом случае для
определения напряжения в какой – либо
точке сечения достаточно разделить
внутреннюю силу Рна площадь сеченияF.
В действительности напряжения равномерно распределяются очень редко и для определения напряжений в точке берут в ее окрестности небольшую площадку ΔF, в пределах которой напряжения можно считать равномерными, и действующую на нее внутреннюю силу ΔРделят на ΔF:
.
Наиболее точно напряжение в точке определяется по формуле:
.
Напряжение текучести
Пластическая деформация тела осуществляется при действии внутренних сил.
Тело под действием внешних сил первоначально деформируется упруго. По мере увеличения внешних сил упругая деформация тела растет, растут внутренние силы, растет напряжение. Для каждой марки стали (сплава) существует свое предельное значение напряжения, по достижении которого упругая деформация тела переходит в пластическую.
Напряжение,
при котором наступает пластическая
деформация, называется напряжением
текучести и обозначается буквой Т.
Физический смысл напряжения текучести
– это сопротивление тела изменению
своей формы и размеров. Иногда напряжение
текучести называют сопротивлением
деформации.
Иногда напряжение
текучести называют сопротивлением
деформации.
При горячей деформации напряжение текучести зависит от 4-х параметров: химического состава стали; температуры деформации; степени деформации; скорости деформации. Чем выше температура деформации, тем ниже значение Т, тем легче деформировать металл. С увеличением степени и скорости деформации Т увеличивается, деформация металла в связи с этим затрудняется.
Для определения напряжения текучести используются графики и расчетные формулы, приведенные в технической литературе.
Ниже приведен метод расчета среднего значения напряжения текучести с использованием термомеханических коэффициентов:
σТ= σ0·kt
где σ0– базисное значение напряжения текучести, учитывающее химический состав металлов;
kt,kε,ku– термомеханические коэффициенты,
учитывающие емпературу, степень и
скорость деформации, определяются из
графиков или рассчитываются по формулам.
Реактивные силы
Внешние силы, действующие на тело, называют активными. Одной из задач теории обработки металлов давлением является определение величины этих сил. Мощность двигателей машин, производящих деформацию, и величину усилий, которые должны развивать эти машины, определяют, исходя из величины усилия, которое необходимо приложить для осуществления деформации. Наряду с активными силами на деформируемое тело действуют реактивные силы, которые возникают в результате создания препятствия движению металла и приложены к инструменту.
Например, приложенная к деформируемому телу сила Р(рис. 3) стремится создать его движение вниз, но этому препятствует возникающая реактивная сила наковальниРр, и движение тела вниз становится невозможным. В теле возникает внутренняя сила, уравновешивающая внешнее приложенное усилие и реактивное давление. В результате появления этой внутренней силы происходит деформация тела.
Рис. | Рис. 4. Осаживание металла в контейнере |
Реактивное давление (инструмента на металл) возникает и в том случае, когда появляется препятствие изменению формы. Если, например, производить осаживание металла в контейнере, то благодаря препятствию, которое создают его стенки уширению металла в горизонтальном направлении, появится горизонтальное реактивное давление стенок контейнера на металл
К внутренним
вертикальным силам, которые уравновешивают
вертикальные деформирующие силы
(приложенное усилие к пуансону Ри
реактивное давление дна матрицыРр),
добавятся горизонтальные внутренние
силы для уравновешивания горизонтальных
реактивных давленийРг.
Реактивные давления возникают всегда
перпендикулярно рабочей поверхности
инструмента. Поэтому в отдельных случаях
направление реактивного давления может
не совпадать с направлением приложенного
усилия. Например, при протягивании
металла через щель, образованную двумя
наклонными поверхностямиААиАБ
Например, при протягивании
металла через щель, образованную двумя
наклонными поверхностямиААиАБ
Рис. 5. Протягивание металла через щель |
Таким образом, при различных направлениях приложенного усилия и реактивного давления возникают различно направленные внутренние силы.
4.4: Второй закон движения Ньютона — концепция системы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 26503
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определить результирующую силу, внешнюю силу и систему.

- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона носит более количественный характер и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорений . Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что суммарная внешняя сила вызывает ускорение .
Сразу возникает другой вопрос. Что мы понимаем под внешней силой? Интуитивное представление о внешнем верное — внешняя сила действует снаружи системы интереса. Например, на рис. \(\PageIndex{1a}\) интересующая нас система — это фургон плюс ребенок в нем. Две силы, действующие со стороны других детей, являются внешними силами. Между элементами системы действует внутренняя сила. Снова взглянув на рисунок \(\PageIndex{1a}\), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе.) 
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и направлено в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было проверено экспериментально и показано на рис. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (в). Для полноты показаны также вертикальные силы; предполагается, что они компенсируются, поскольку ускорение в вертикальном направлении отсутствует. Вертикальные силы — это вес \(w\) и опора земли \(N\), а горизонтальная сила \(f\) представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах. Сейчас мы определим трение как сила, противодействующая движению друг относительно друга соприкасающихся объектов. На рисунке \(\PageIndex{1b}\) показано, как векторы, представляющие внешние силы, складываются вместе, образуя результирующую силу \(F_{net}\).
Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения и чистой внешней силы как пропорциональность
\[ a \propto F_{net} \]
где символ \( \propto \) означает «пропорционально», а \(F_{net} \) — это чистая внешняя сила . (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для добавления других векторов, и рассматриваются в разделе главы о двумерной кинематике.) Эта пропорциональность утверждает то, что мы сказали словами: ускорение прямо пропорционально суммарной внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для добавления других векторов, и рассматриваются в разделе главы о двумерной кинематике.) Эта пропорциональность утверждает то, что мы сказали словами: ускорение прямо пропорционально суммарной внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на рисунке, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
И действительно, как показано на рисунке, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
\[ a \propto \dfrac{1}{m}, \]
, где \(m\) — масса системы. Эксперименты показали, что ускорение точно обратно пропорционально массе, так же как оно точно линейно пропорционально суммарной внешней силе.
Рисунок \(\PageIndex{2}\): Одна и та же сила, действующая на системы с разной массой, создает разные ускорения. а) Баскетболист толкает мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (b) Тот же игрок прикладывает такую же силу к заглохшему внедорожнику и создает гораздо меньшее ускорение (даже если трением можно пренебречь). (c) Диаграммы свободного тела идентичны, что позволяет проводить прямое сравнение двух ситуаций. Ряд паттернов для диаграммы свободного тела появится по мере того, как вы будете решать больше задач. Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Сочетание двух только что приведенных пропорций дает второй закон движения Ньютона.
Сочетание двух только что приведенных пропорций дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально внешней силе, действующей на систему, и имеет то же направление, что и обратно пропорционально ее массе. В форме уравнения второй закон Ньютона равен 9.0032
\[ a = \dfrac{F_{net}}{m}\]
Это часто записывается в более знакомой форме
\[ F_{net} = ma. \]
Когда учитываются только величина силы и ускорения, это уравнение просто
\[ F_{net} = ma. \]
Хотя последние два уравнения на самом деле одинаковы, первое дает более полное представление о том, что означает второй закон Ньютона. Закон представляет собой причинно-следственную связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке. 92 \]
В то время как почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее распространенной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую ее вес \(w\). Вес можно обозначить как вектор \(w\), потому что он имеет направление; вниз по определению является направлением силы тяжести, и, следовательно, вес является направленной вниз силой. Величина веса обозначается как \(w\). Галилей сыграл важную роль в том, чтобы показать, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением \(w\). Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой \(m\), падающий вниз к Земле. Он испытывает только направленную вниз силу тяжести, которая имеет величину \(w\). Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна \(F_{net} = ma\). 92) = 9,8 Н. \]
92) = 9,8 Н. \]
Напомним, что \(g\) может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учитывайте это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует восходящая сила воздуха. 92\). Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и действительной невесомостью.
Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и действительной невесомостью.
Важно помнить, что вес и масса — очень разные физические величины, хотя и тесно связанные между собой. Масса — это количество материи (сколько «вещества») и не меняется в классической физике, тогда как вес — это гравитационная сила, которая зависит от гравитации. Заманчиво приравнять их, поскольку большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, термы масса и веса взаимозаменяемы в повседневном языке; например, наши медицинские записи часто показывают наш «вес» в килограммах, но никогда в правильных единицах измерения — ньютонах.
РАСПРОСТРАНЕННЫЕ ЗАБЛУЖДЕНИЯ: МАССА VS. ВЕС
Масса и вес часто используются как синонимы в повседневном языке. Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте. Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта \((m)\), умноженной на ускорение свободного падения \((g)\). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения). 92\) ). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, приводит к тому, что они весят меньше)
Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте. Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта \((m)\), умноженной на ускорение свободного падения \((g)\). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения). 92\) ). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, приводит к тому, что они весят меньше)
ВОЗМОЖНЫЙ ЭКСПЕРИМЕНТ: МАССА И ВЕС
Что делают напольные весы мера? Когда вы встаете на напольные весы, что происходит с весами? Это слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9.80, чтобы дать показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?
Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9.80, чтобы дать показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?
Пример \(\PageIndex{1}\): Какое ускорение может создать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Каково его ускорение?
Рисунок \(\PageIndex{3}\): Чистая сила, действующая на газонокосилку, равна 51 Н вправо. С какой скоростью газонокосилка ускоряется вправо?Стратегия
Поскольку \( F_{net} \) и \( m \) заданы, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в \( F_{net} = ma \).
Решение
Величина ускорения \(a\) равна \(a = \frac{F_{net}}{m}\). Ввод известных значений дает \[ a = \dfrac{51 \, N}{24 \, кг} \] 92 \]
Обсуждение
Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны уравновешиваться, если не должно быть ускорения в вертикальном направлении (ускорение в вертикальном направлении). косилка движется только горизонтально). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример \(\PageIndex{2}\): Какая реактивная тяга ускоряет эти сани?
До пилотируемых космических полетов ракетные салазки использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Вычислите величину силы, действующей на каждую ракету, называемую ее тягой \(Т\), для четырехракетной двигательной установки, показанной на рисунке. Начальное ускорение саней равно \(492\) масса системы 2100 кг, а сила трения, противодействующая движению, известна как 650 Н.
Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Вычислите величину силы, действующей на каждую ракету, называемую ее тягой \(Т\), для четырехракетной двигательной установки, показанной на рисунке. Начальное ускорение саней равно \(492\) масса системы 2100 кг, а сила трения, противодействующая движению, известна как 650 Н.
Стратегия
Хотя существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения.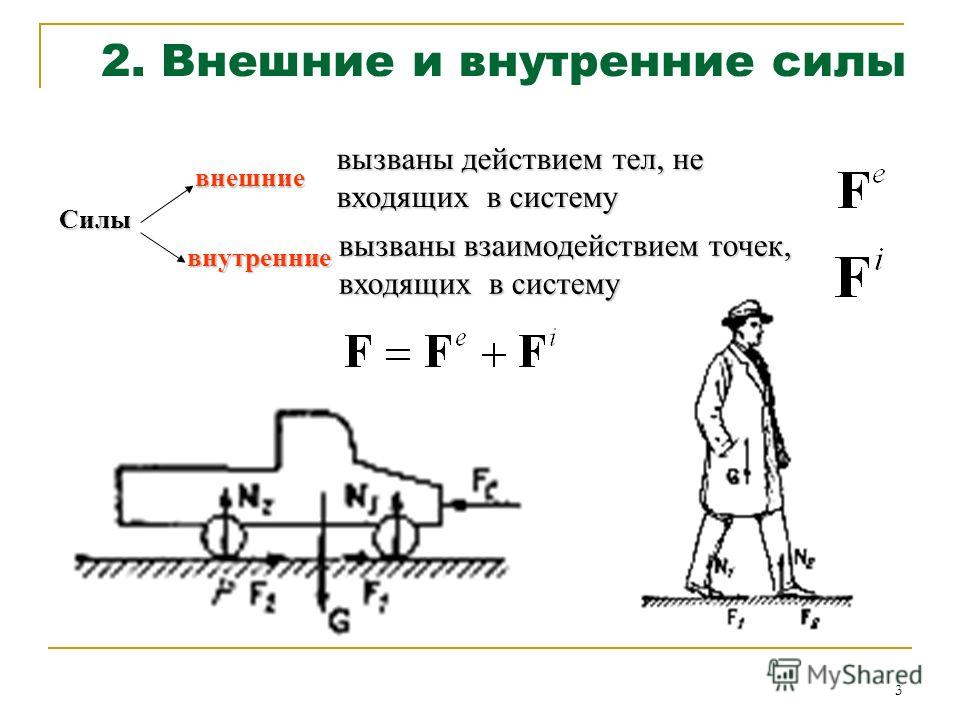 Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.
Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения известны, начнем со второго закона Ньютона и будем искать способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с \[ F_{net} = ma. \], где \(F_{net}\) — результирующая сила в горизонтальном направлении. Из рисунка видно, что тяги двигателя складываются, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна \[ F_{net} = 4T — f. \] 92\) ). В то время как живые объекты больше не используются, с помощью ракетных саней была достигнута наземная скорость 10 000 км/ч. В этом примере, как и в предыдущем, интересующая система очевидна.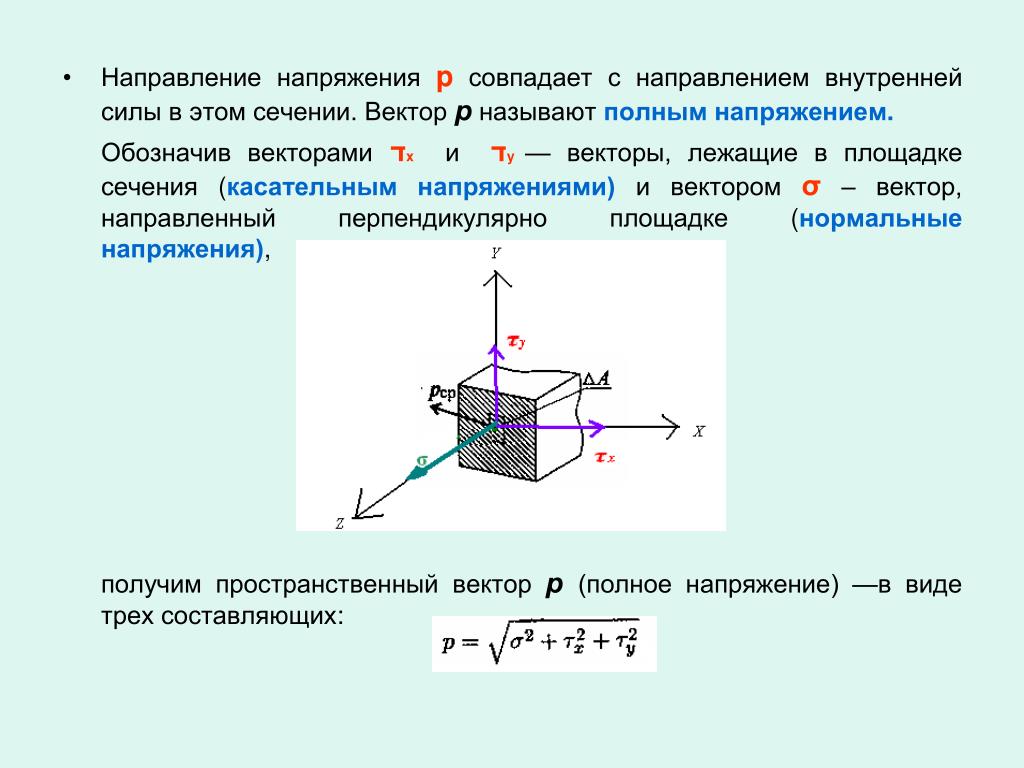 В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Резюме
- Ускорение, \(a\), определяется как изменение скорости, что означает изменение ее величины или направления, или того и другого.
- Внешняя сила — это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе.

- В форме уравнения второй закон движения Ньютона имеет вид \( a = \frac{F_{net}}{m} \)
- Это часто записывается в более привычной форме: \( F_{net} = ma. \)
- Вес \(w\) объекта определяется как сила тяжести, действующая на объект массой \(m.\). Объект испытывает ускорение под действием силы тяжести \(g\): \[ w = mg. \]
- Если единственная сила, действующая на объект, связана с гравитацией, объект находится в свободном падении.
- Трение — это сила, препятствующая движению соприкасающихся объектов относительно друг друга.
Template:HypTest
Эта страница под названием 4.4: Второй закон движения Ньютона. Концепция системы распространяется по лицензии CC BY и была создана, изменена и/или курирована OpenStax.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Встроенный CalcPlot3D?
- да
- Встроить Hypothes.
 is?
is? - да
- Лицензия
- СС BY
- Показать оглавление
- да
- Включено
- да
- Теги
- 2-й закон
- Сил
- источник[1]-физ-1499
- система
49 Важные факты, которые вы должны знать —
Мы испытываем силу трения каждый день в нашей жизни. В этом посте мы обсудим несколько сила трения примеров из нашей повседневной жизни в деталях.
Force Of Friction Examples- Sliding an object
- Dragging a heavy material
- While you walk
- Rolling Ball stops automatically
- Трение метеора при входе в атмосферу Земли
- Альпинические растения
- Поток чернил в ручках
- Главная рубашка
- Главная рубашка
- ТУР.

- Очистка поверхности жидкостями
- Парашютист
Примером силы трения является скольжение любого предмета по столу. Когда вы двигаете предмет по столу, он приходит в исходное положение через определенное время из-за силы трения.
Изображение предоставлено pixabay free images Перетаскивание тяжелого материала.Становится сложно перемещать тяжелые материалы ; мы должны применить силу , чтобы перетащить его. Это означает, что сила в противоположном направлении имеет большую величину, чем приложенная сила. Следовательно, чтобы сдвинуть этот материал, требуется сила, превышающая сила трения должна быть приложена.
Изображение предоставлено: «Путешественник по миру» Мики Ситтига под лицензией CC BY 2.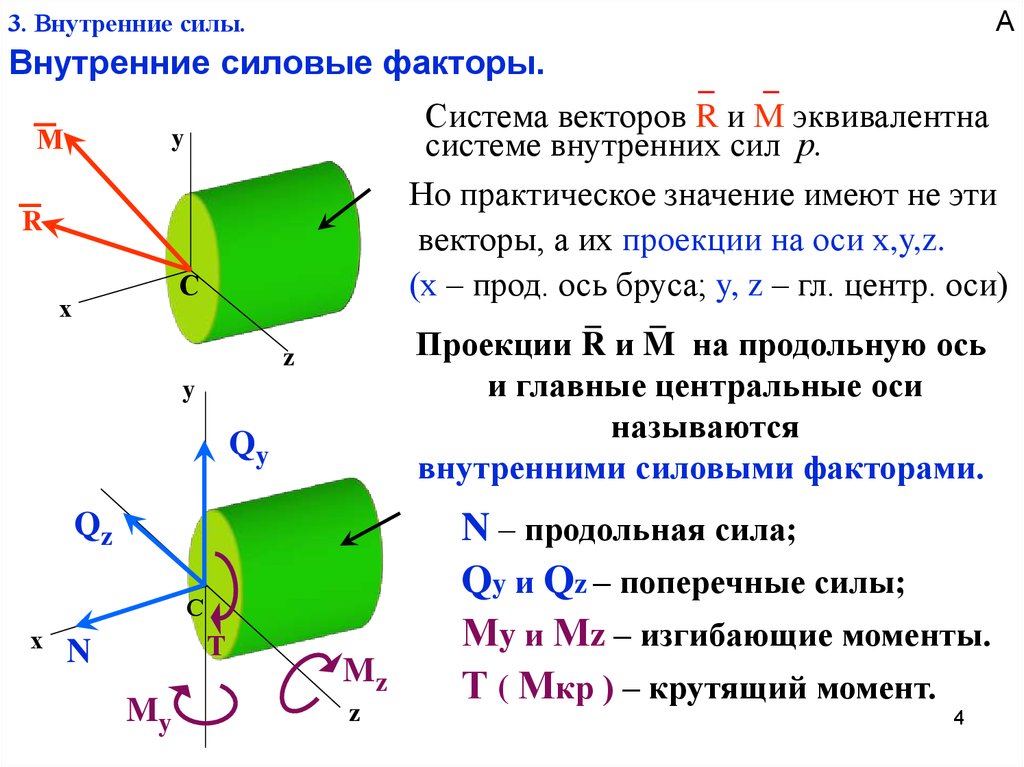 0 Пока вы идете.
0 Пока вы идете. Во время ходьбы мы обычно испытываем силу трения. Ходьба происходит только из-за наличия трения между ногами и землей. Это создает сцепление между ними, которое помогает нам двигаться вперед. Здесь сила, приложенная ногой, равна и противоположна силе трения, создаваемой землей.
Изображение предоставлено pixabay free images Катящийся шарик автоматически останавливается .Когда вы прикладываете силу к мячу, он начинает катиться, но через определенное время скорость мяча уменьшается, и он останавливается. Это изменение скорости происходит за счет силы трения .
Изображение предоставлено: «Rolling The Ball» от Dark Dwarf под лицензией CC BY-ND 2.0 Трение, испытанное метеором. До входя в атмосферу земли, метеоры испытывают высокую силу трения , и благодаря этому сгорают перед падением на поверхность земли.
Многие вьющиеся растения в природе взбираются на поверхность деревьев с помощью силы трения . Как правило, для лазания они используют грубые поверхности, такие как ствол и кора дерева.
Изображение предоставлено pixabay free images Поток чернил в ручках.Течение чернил в ручке происходит из-за силы трения, называемой трением жидкости. Поток жидкости через поверхности испытывает трение, а вязкость чернил снижается для разумной скорости потока.
Изображение предоставлено pixabay free images Глажка рубашки. Без силы трения железный ящик скользил бы через ткань, когда вы пытаетесь ее погладить. Действительно, трение — это явление, которое помогает оказывать давление на сморщенную ткань; здесь давление является одним из влияющих факторов трения и прямо пропорционально трению.
В игре перетягивание каната , в которую обычно играют как в забаву, две команды тянут друг друга с помощью твердой веревки между ними. Много здесь задействована сила трения между рукой игроков и веревкой.
Изображение предоставлено pixabay free images Шкив для забора воды из колодца.Сила трения между шкивом и канатом обеспечивает прочное сцепление, позволяющее удерживать ковш. В общем, чтобы достать воду из колодца, мы используем веревку и ведро, соединенное с помощью шкива. Трение помогает нам тянуть воду из колодца.
Изображение предоставлено: «Подача воды из деревенского колодца, Южная Суматра, Индонезия, 2006 г. Фото: Рани Ноэрхадхи/AusAID» из фотобиблиотеки DFAT, лицензия CC BY 2. 0 Очистка поверхности жидкостями.
0 Очистка поверхности жидкостями. Некоторые жидкости обычно используются для мытья поверхностей, поскольку они помогают уменьшить силу трения между частицами пыли и поверхностью, делая поверхность чистой.
Изображение предоставлено: «Уборка пола» от tinafranklindg под лицензией CC BY 2.0 Skydiver.Парашютист испытывает много сил трения во время пикирования с воздуха. Во время погружения его скорость увеличивается на , и для выполнения таких трюков человек должен быть в хорошей физической и умственной форме.
Изображение предоставлено pixabay free images Примеры увеличения трения.Если поверхность шероховатая, она испытывает большее трение и большее сцепление . Примеры увеличения трения следующие:
Распространение песка.
После дождя поверхность становится скользкой ; она сделана шероховатой из-за того, что разбрасывает песок, чтобы увеличить трение , чтобы по ней было легко ходить.
Изображение предоставлено: «130110-A-ON889-168» norfolkdistrict лицензируется в соответствии с CC BY 2.0
Шины с протектором.Шины транспортных средств имеют особый тип конструкции, называемый протекторами , которые видны на их поверхности. Это помогает увеличить трение между землей и шиной.
Изображение предоставлено pixabay free images Гимнастки.Гимнасты обычно наносят на руки специальный грубый материал, чтобы получить надежный захват. Этот материал курса помогает увеличить трение между их руками и предметами, которые они используют для исполнения.
Изображение предоставлено pixabay free images Футбольные бутсы с шипами.
Футбольные бутсы оснащены уникальными шипами , которые увеличивает трение и помогает игрокам лучше сцепляться с землей и обувью. Если бы шипы не были спроектированы, существовала вероятность того, что они могли бы соскользнуть во время игры.
Изображение предоставлено: pixabay free images Кабадди-игрок вытирает руки песком.Перед игрой в кабадди игроки обычно вытирают руки песком до увеличивают трение . Кроме того, это помогает им закрепиться на игроке противоположной команды.
Изображение предоставлено: «kabbadi kabbadi» от Unlisted Sightings под лицензией CC BY 2.0 Подошва обуви с бороздками.Поверхность наших сандалий имеет бороздки —, увеличивающие трение , что помогает нам комфортно ходить по дорожке.
Изображение предоставлено pixabay free images Примеры уменьшения трения.
Мы создаем более гладкую поверхность , потому что она уменьшает трение и объекты перемещаются далеко с меньшим сцеплением. Примеры уменьшения трения :
Применение смазочных материалов.
Применяя смазочные материалы, такие как смазка или масло , мы можем уменьшить силу трения между движущимися частями двигателя транспортного средства. В результате уменьшается износ деталей и продлевается их срок службы.
Наносим масло на дверные ручки с по уменьшают трение , чтобы сделать движение плавным и легким. Применяемое здесь масло превращает сухое трение в жидкостное.
Изображение предоставлено: «Project 365 #311: 071118 Smooth Operator» от Comedy_nose под лицензией CC BY 2. 0 Полировка поверхности.
0 Полировка поверхности. Неровность поверхности можно уменьшить полировкой ; здесь полировка уменьшает трение , нанося масла на дверные ручки, чтобы сделать движение управляемым.
Изображение предоставлено: pixabay free images Использование шарикоподшипника.Шариковые подшипники обычно используются для уменьшения трения во вращающихся машинах . Хотя трение качения будет меньше трения скольжения, когда валы установлены на шарикоподшипниках, оно уменьшает трение .
Изображение предоставлено: «Сферические шарикоподшипники @ 100 Innovationer @ Tekniska Museet» от pellesten под лицензией CC BY 2.0 Оптимизация. Обтекаемость тел уменьшает силу трения . Например, трение о воздух уменьшается благодаря конструкции обтекаемых корпусов самолетов; Точно так же гидравлическое трение уменьшается, если конструкция корпуса корабля обтекаема.
Высокое трение обычно подходит для сухих и шероховатых поверхностей ; это очень высоко, что заставляет объекты замедляться. Примеры с высоким коэффициентом трения:
Езда на велосипеде по дороге.Трение помогает двигаться, трогаться с места, останавливаться и поворачивать велосипед . Это высокое трение гарантирует, что вы не соскользнете с дороги. Благодаря высокому трению конструкция шин обеспечивает столь необходимое сцепление для цикла.
Изображение предоставлено: pixabay free images Износ обуви.Высокое трение вызывает износ обуви . То самое трение, которое помогает нам ходить, если оно увеличивается, может повредить вашу обувь.
Тормоза автомобилей.
Шины автомобиля сделаны шероховатыми для увеличения трения . Тормоза автомобиля всегда работают за счет трения между колесом и тормозной колодкой. Здесь высокое трение помогает замедлить движение транспортного средства.
Изображение предоставлено pixabay free images Потирание рук.Потирание рук является повседневным примером сильного трения . Когда мы потираем руки, мы чувствуем, как наши руки становятся теплее; здесь высокое трение производит тепловую энергию, что дает нам ощущение тепла.
Геккон на стене. Ящерица-геккон — хороший пример высокого трения .
С помощью силы трения ящерице-геккону будет легко взобраться на стену, потому что между ее ногами и поверхностью стены действует высокое трение.

Когда человек пытается взобраться на скалу, он испытывает сильное трение . Эта сила трения помогает установить прочное сцепление между его ступнями, руками и поверхностью камня. И это также предотвращает его от случайного скольжения.
Изображение предоставлено: «Будущий военнослужащий взбирается на каменную стену» штаб-квартиры USACE, помечен CC PDM 1.0 Зажигание спички.Когда мы проводим спичкой по шероховатой поверхности спичечного коробка, создается сильное трение , что вызывает зажигание спички . Это происходит за счет нагревательного эффекта трения .
Изображение предоставлено pixabay free images Лесные пожары. Лесные пожары возникают из-за сильного трения , возникающего при трении двух деревьев друг о друга. Это происходит из-за теплового эффекта трения, приводящего к пожару.
Низкое трение обычно действует на гладкие и влажные полы и обеспечивает движение предметов. Например, в следующих примерах обычно наблюдается низкое трение.
Ходьба по маслянистой или скользкой поверхности.При ходьбе по мокрой или маслянистой поверхности становится трудно сохранять равновесие при ходьбе. Жидкость на поверхности снижает коэффициент трения (низкое трение), что приводит к слабому сцеплению ног с поверхностью, что приводит к несчастному случаю.
Изображение предоставлено pixabay free images Carrom Board. Когда боек скользит по карамбольной доске , боек испытывает трение . Здесь сила трения представляет собой малое трение , которое замедляет скорость бойка и иногда может сопротивляться его движению. Как правило, присыпка снижает трение и обеспечивает плавное движение бойка по поверхности.
Как правило, присыпка снижает трение и обеспечивает плавное движение бойка по поверхности.
Летающие птицы являются естественным примером низкого трения. Это потому, что у птиц легкое и идеально сконструированное тело, чтобы уменьшить трение .
Воспроизведение скольжения является примером трения скольжения . Скольжение уменьшает коэффициент трения и делает поверхность скользкой, что обеспечивает низкое трение и предотвращает падение и травмы. Таким образом, скольжение дает нам захватывающий опыт без какого-либо вреда.
Изображение предоставлено pixabay free images Сани скользят. Сани, скользящие по льду или ходьба по льду, являются примером кинетического трения . Лед, присутствующий на поверхности, уменьшает силу трения между человеком и поверхностью. Это низкое трение заставляет человека очень плавно скользить или скользить по поверхности.
Лед, присутствующий на поверхности, уменьшает силу трения между человеком и поверхностью. Это низкое трение заставляет человека очень плавно скользить или скользить по поверхности.
Катание шара для боулинга является примером трения качения . Когда вы катите мяч по дорожке, мяч испытывает низкое трение, что позволяет легко перекатиться по дорожке и попасть в цель.
Изображение предоставлено: «Ник пытается научить ее «катать» мяч». от JenCarole лицензируется в соответствии с CC BY-ND 2.0 Примеры ограничения трения.Предельное трение — максимальное трение, которого достигает тело; после достижения этого значения тело движется дальше. Примеры предельного трения :
Автомобиль на холме.
Транспортное средство на горе/холме не будет двигаться вниз при парковке , и это происходит из-за высокого значения предельного трения ; это заставляет автомобиль оставаться в состоянии покоя . В общем случае предельное трение прямо пропорционально массе тела.
Изображение предоставлено pixabay free images Надпись на книге.Мы можем писать на книге или чем-то еще из-за ограничения трения . Сила трения между ручкой и книгой заставляет частицы склеиваться на книге.
Изображение предоставлено: pixabay free images
Перемещение объекта по земле. Трудно передвигать тяжелый предмет. Это связано с тем, что когда приложенная сила увеличивает , статическое трение , а также увеличивает , и после того, как оно достигает значения предельного трения, объект начинает двигаться.
Толкать груженый автомобиль — очень сложная задача . Это связано с тем, что значение статического трения в начале очень высокое . Однако иногда оно достигает значения предельного трения, при котором становится менее трудно толкать транспортное средство.
Изображение предоставлено: «Вы должны карабкаться на фасад здания, даже когда проезжают две велорикши!» автор: shankar s, CC BY 2.0 Часто задаваемые вопросы |Часто задаваемые вопросы Что такое сила трения?Иногда нам трудно перемещать объекты.
Это происходит потому, что противодействующая сила сопротивляется движению, такая сила называется трением, которая действует, когда две поверхности соприкасаются друг с другом. В результате уменьшается й е скорость тела в движении .
В результате уменьшается й е скорость тела в движении .
Коэффициент трения всегда зависит от типа используемых материалов.
Коэффициент трения между поверхностями описывается как отношение предельного трения к нормальной силе, действующей между ними.
Коэффициент трения =
Коэффициенты трения варьируются от нуля до больше единицы.
Что такое трение качения?Трение качения — это сила трения, возникающая, когда объект катится по поверхности.
Эта сила трения вообще противодействует движению тела, которое катится по земле; i t зависит от массы тела.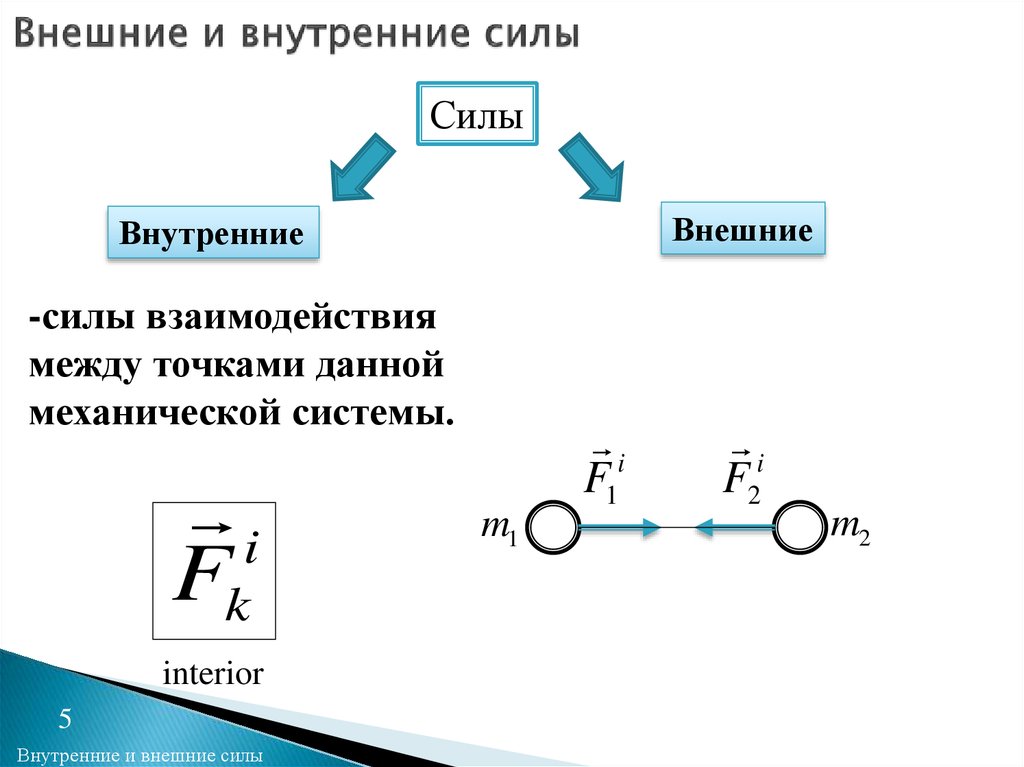 Например, это происходит, когда шар, цилиндр катятся по поверхности.
Например, это происходит, когда шар, цилиндр катятся по поверхности.
Статическое трение — это сила трения, которая заставляет тело оставаться в состоянии покоя.
Сила трения возникает, когда мы пытаемся толкнуть неподвижный объект, фактически не нарушая относительного движения между телом и поверхностью.
Некоторые факторы, влияющие на трение, следующие:
- Характер скользящего объекта.
- Характер поверхности.
- Дизайн или форма объекта.
- Состояние вещества объекта.
- Площадь соприкасающихся поверхностей.
- Характер задействованного трения.
Около преимуществ и недостатков трения являются следующими,
| Преимущества | Диссыпания |
| We W We Tow0047 | Шины и колодки рвутся.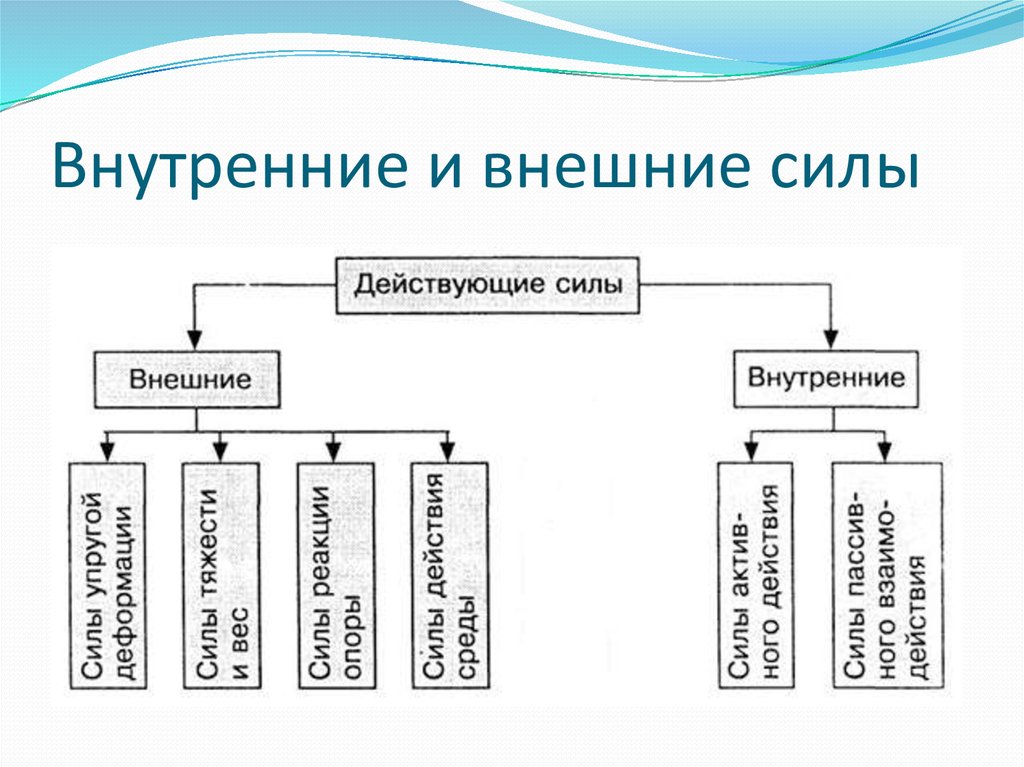 |

 3. Свободное
осаживание цилиндра
3. Свободное
осаживание цилиндра

 is?
is?