Социально-методический центр поддержки СО НКО Московской области

Эрудит (игра) | это… Что такое Эрудит (игра)?

Толкование

Эрудит (игра)

Скрэббл (англ. Scrabble — «рыться в поисках чего-либо») — настольная игра, в которую могут играть от 2 до 4 человек, выкладывая слова из имеющихся у них букв в поле размером 15 x 15. В русскоязычной среде известна под названием «Эрудит».

Содержание 1 Правила 1.1 Словарь 1.2 Игра 1.3 Подсчет очков и бонусы 1.4 Пустышка (джокер, «звёздочка») 2 История 3 Различия между «Эрудит» и «Скрэббл» 4 Модификации игры 5 Ссылки

Правила

Игровое поле состоит из 15х15, то есть 225 квадратов, на которые участники игры выкладывают буквы, составляя тем самым слова. В начале игры каждый игрок получает 7 случайных букв (всего их в игре 100).

На середину игрового поля выкладывается первое слово, затем следующий игрок может добавить слово «на пересечение» из своих букв. Слова выкладываются либо слева направо, либо сверху вниз.

Словарь

Разрешается использовать все слова приведенные в стандартном словаре языка за исключением слов пишущихся с прописных букв, сокращений, и слов, которые пишутся через апостроф или тире. В варианте «Скрэббл» можно использовать все падежи, склонения и времена.

В то же время в игре «Эрудит» согласно традициям русских лингвистических игр разрешено использовать только имена существительные нарицательные в именительном падеже единственного числа (либо множественного при отсутствии у слова формы единственного числа).

Запрещено использовать словарь для поиска слов. Словарь разрешен только в случае проверки на существование уже выложенного слова.

Игра

• В начале игры каждому дается по 7 фишек. За один ход можно выложить несколько слов. Каждое новое слово должно соприкасаться (иметь общую букву или буквы) с ранее выложенными словами.
  Слова читаются только по горизонтали слева направо и по вертикали сверху вниз.
• Первое выложенное слово должно проходить через центральную клетку.
• Если игрок не хочет или не может выложить ни одного слова, — он имеет право поменять любое количество своих букв, пропустив при этом ход.
• Любая последовательность букв по горизонтали и вертикали должна являться словом. Т.е. в игре не допускается появление на поле случайных буквосочетаний, не представляющих собою слов, соответствующих вышеприведенным критериям.
• После каждого хода необходимо добрать новых букв до 7.
• Если за ход игрок использовал все 7 косточек, то ему начисляются дополнительные 50 очков.

Подсчет очков и бонусы

Каждой букве присвоено некоторое количество очков от 1 до 10. Некоторые квадраты на доске раскрашены в разные цвета. Количество очков, получаемых игроком за выложенное слово, подсчитывается следующим образом:

• если квадрат под буквой бесцветен, добавляется количество очков, написанное на букве
• если квадрат голубой, количество очков буквы умножается на 2
• если квадрат розовый, количество очков всего слова умножается на 2
• если квадрат синий, количество очков буквы умножается на 3
• если квадрат красный, количество очков всего слова умножается на 3

Если слово пересекает и красную и синюю клетки, то в удвоении (утроении) очков слова учитывается удвоение (утроение) очков букв.

Пустышка (джокер, «звёздочка»)

Также, в наборе косточек присутствует несколько пустых фишек (в версии «Эрудит» — звёздочек). Такая фишка может быть использована как любая буква на выбор игрока. Например, игрок может выставить слово «ТЕ*ЕФОН», где роль буквы «Л» будет играть пустышка.

Правила подсчета очков и использования пустышек могут отличаться и игрокам следует заранее договориться о нюансах. Ниже приведены возможные варианты правил.

Подсчет очков за пустышку:

• Пустышка всегда имеет 0 очков (классические правила Scrabble).
• Пустышка приносит столько очков, сколько бы принесла буква, роль которой она играет.

Повторное использование пустышек:

• После выкладывания на поле, пустышка считается сыгранной и так и остается на этом месте до конца партии (классические правила Scrabble).
• Если один игрок выложил слово «ТЕ*ЕФОН», то затем, любой игрок, имея у себя букву «Л», может заменить ее на пустышку и забрать ее себе. Как правило, действует дополнительное правило, обязывающее в таком случае использовать (выложить) забранную с поля пустышку этим же ходом, т.е. когда нельзя брать ее себе «про запас».

История

Игра была изобретена в 1938 году архитектором Альфредом Баттсом. В США и многих странах Европы до сих пор проводятся регулярные чемпионаты по Скрэбблу.

Различия между «Эрудит» и «Скрэббл»

Параметр	«Скрэббл»	«Эрудит»
«универсальная» фишка	пустышка	звездочка
цвета бонус-клеток	голубой, синий, розовый, красный	зеленый, голубой, желтый, красный
различная стоимость букв	Ю:8	Ю:10
буква «Ё»	присутствует	отсутствует
количество фишек	104	129

Модификации игры

• «Найди слово» — модификация игры с немного измененным полем (прямоугольным).
• Математический скрэббл

Ссылки

• Список компьютерных версий игры Скрэббл

• Эрудит (русский аналог Scrabble)

Интеллектуальные игры
«Бескрылка» | «Брейн-ринг» | Бридж | «Завалинка (Надуваловка)» | Го | Преферанс | Рэндзю | «Своя игра» | Судоку | «Что? Где? Когда?» (теле) (спорт) | Шахматы | Шашки | «Эрудит»(«Скрэббл») | «Эрудит-Квартет»

Wikimedia Foundation. 2010.

Нужна курсовая?

• Эруэн Анри
• Эрхай (озеро)

Полезное

Анатолий Вассерман – биография, фото, личная жизнь, семья, дети, взгляды, рост и вес 2022

Биография Анатолия Вассермана

Анатолий Александрович Вассерман – человек-уникум, известный в Советском Союзе как инженер, в 90-е – как участник интеллектуальных игр «Что? Где? Когда?», «Своя игра» (становился чемпионом игры 15 раз кряду), «Брейн-ринг».

В середине 2000-х личность Вассермана получила популярность в интернете благодаря пришедшему с «Упячки» мему «Онотоле» и шуткам про его жилетку с карманами.

На фото: Анатолий Вассерман

Теперь Вассермана знают еще и как публициста, писателя, политического консультанта, блогера и телеведущего. Вел собственный блог в Живом Журнале и развлекательное шоу «Вынос мозга» на YouTube, куда приглашал кумиров молодежи – рэперов и блогеров. Совместно с братом Владимиром написал и издал несколько интереснейших книг об Одессе.

Детство и семья

Когда зимой 1952 года в одесской семье ученого-теплофизика Александра Вассермана и бухгалтера-экономиста Лины Ильиничны Баум родился мальчик, его назвали Анатолием – в честь дедушки, военного врача.

Анатолий Вассерман с родителями

Дед, Анатолий Соломонович, практически всю свою жизнь провел в Красной армии: сначала помощником врача на Гражданской войне в 1919-1920 годах, затем, по окончании Одесской медакадемии, служил врачом в 51 Перекопской дивизии. С 1926 года работал в школе артиллеристов, а после демобилизации стал районным терапевтом. В 1939 году его снова призвали в армию.

Героический дедушка Анатолия Вассермана

На Финской войне служил врачом в Щорсовской дивизии, лечил обморозившихся и больных солдат Красной армии, вывозил из окружения раненных. Позже его внук рассказывал, что дедушку даже представили к ордену Красной Звезды, что для 1940 года было очень почетно. Но поскольку командир дивизии был расстрелян за пассивность в окружении, Анатолий Соломонович так и не получил свою заслуженную награду.

В Великой Отечественной войне военврач Вассерман получил тяжелую контузию, демобилизован из армии за год до Победы, а в 1949 году скончался, за три года до рождения внука, который очень хорошо запомнил табличку с надписью на дверях:

На дверях нашего одесского родового гнезда до сих пор висит табличка «Вассерману звонить 1 раз». Она исполнена золотыми буквами на тыльной стороне толстого стекла, а затем поверх букв залита тушью, чтобы буквы лучше выглядели на черном фоне. После смерти деда слово «доктору» над фамилией старательно зачищено от золота и замазано той же тушью.

Бабушка Толи, Либа Хаймовна (Любовь Ефимовна) Кизер-Вассерман, иногда забирала малыша в туберкулезный санаторий «Аркадия», где работала врачом-фтизиатром более тридцати лет и была удостоена звания «Отличник здравоохранения».

Отец, доктор технических наук, был погружен в науку и преподавательскую работу. Толе до восьми лет было предоставлено домашнее обучение (которым занималась мама), поскольку в детстве он был слабым ребенком и постоянно болел. Её методика принесла плоды: бегло читать мальчик умел уже в четыре года, а в четырнадцать самостоятельно прочел 15-томный справочник машиностроения и попытался объяснять своему младшему на восемь лет брату Володе, что как устроено и почему.

Анатолий Вассерман в детстве

Его увлек манящий мир инженерных конструкций, особенно врезался в память и понравился подростку термин «ковочные вальцы», которым он бравировал среди сверстников и который означал вид металлообработки.

Анатолий Вассерман с младшим братом и отцом

В общеобразовательную школу Толя пришел сразу во второй класс, но все так же часто болел и пропускал уроки. По сути, учеба продолжалась на дому. А когда приходил в класс, то делал домашние задания для нескольких мальчишек, которые насмехались над нескладным и вечно болеющим очкариком. Толю даже перевели в другую школу из-за этого. Чем старше становился мальчик, тем больше проблем у него возникало в школе: уже не только со сверстниками, но и с учителями, которых он мог поправить по ходу урока, объясняя вместо них предмет.

Образование

Эрудиция и сверхпрограммный объем знаний сыграли с Анатолием злую шутку: аттестат был самый обычный, отличником Вассерман так и не стал. Но зато сразу после школы играючи стал студентом Одесского технологического института холодильной промышленности. На третьем курсе написал первую компьютерную программу для решения конкретной задачи (а не для учебных целей), а ведь на дворе стоял 1972 год.

Анатолий Вассерман в молодости

В институте заинтересовался и политикой. Перечитал для начала от корки до корки Собрание сочинений Карла Маркса и Фридриха Энгельса, а затем последовательно проштудировал труды Владимира Ленина.

Со специальностью «инженер-теплофизик» Анатолий окончил вуз и поступил на работу в НПО «Холодмаш». По тем временам новое слово «программист» только входило в сферу профессий, а Вассерман, проработав три года в «Холодмаше» перешел в НИИ «Пищепромавтоматика» на должность системного программиста.

Интеллектуальные игры

Энциклопедические обширные знания привели сотрудника НИИ в отборочные соревнования интеллектуальной телевизионной игры «Что? Где? Когда?» В 1989 году состоялся его дебют на всесоюзном телевидении. На протяжении нескольких лет он был членом команды Нурали Латыпова.

Что? Где? Когда? Выпуск с Анатолием Вассерманом (1991)

Когда его пригласили в одесскую команду Виктора Мороховского вместе с еще одним интеллектуалом, Борисом Бурдой, они стали ярким и запоминающимся тандемом в «Брейн-ринге», новой передаче на телевидении.

Анатолий Вассерман с товарищами по «Брейн-рингу»

Но самым блестящим стало его участие в еще одном соревновании интеллектов на ТВ под названием «Своя игра». В нем Анатолий стал первым рекордсменом, выиграв пятнадцать раз подряд и получив заслуженное звание «Лучший игрок десятилетия». Казалось бы, можно и возгордиться, но Вассерман с присущим ему чувством самоиронии не зазнался и в одном из интервью объяснил почему:

Когда почти три десятка лет участвуешь в интеллектуальных играх, очень сложно ощутить свое превосходство. Ведь в них есть не только победы, но и поражения. Есть такой анекдот про Израиль. Его обычно рассказывают среди тех, кто задумывался об эмиграции. Анекдот такой. Над входом аэропорта Бен-Гурион висит плакат с надписью: «Имейте в виду, здесь все такие умные». А так как я постоянно нахожусь в среде где «все такие умные», – начисто отучился от зачатков превосходства над окружающими.

Подтверждением его слов стало участие Вассермана и в менее известных телевизионных играх – «Знатокиаде», «Играх разума», где он выступал в роли соперника гостей шоу.

Вассерман – один из лучших игроков «Своей игры»

Личность уникального эрудита стала практически «народным достоянием», о котором стали сочинять байки и анекдоты, «Факты про Вассермана», публиковать мемы. Сам знаменитый «знаток» вполне лояльно отнесся к такой неоднозначной своей популярности и даже участвовал в вирусной рекламе интернет-магазина, в которой избавился от своего неотъемлемого атрибута – жилетки с множеством карманов.

Анатолий Вассерман в рекламе

Журналист и политконсультант

Знаменитый эрудит не раз заявлял, что занимается лишь тем, что его по-настоящему увлекает, и что вся его работа – часть его многочисленных хобби. Очередным таким хобби Вассермана, переросшим в работу, стало поприще политической журналистики и публицистики.

Весьма категоричный в некоторых суждениях, Анатолий вызвал «огонь на себя», когда решил баллотироваться в Верховную Раду Украины. Его заявления о том, что украинский язык всего лишь диалект русского, а также о том, что Украине надо присоединиться к России, не дали ему возможности набрать нужное количество голосов в 1994 году, чтобы проявить себя на политической арене Украины.

Несколько позже пошли слухи о том, что Вассерман может предложить свою кандидатуру на пост мэра Одессы, но никаких подтверждений или опровержений с его стороны не последовало, и пресса утихла. Анатолий тем временем перебрался в Москву и стал давать политические консультации многим известным как в ту пору, так и сегодня, политикам. Параллельно публиковал в различных изданиях свои статьи, а затем стал вести блог в Живом Журнале, где со свойственным ему свободомыслием размещал собственные размышления, мнения, заметки.

Вассерман о будущем Украины

Интеллектуал не придерживался четкого расписания. Обычный рабочий день для Вассермана в то время зависел от намеченных и незапланированных встреч, погоды, наличия или отсутствия продуктов в холодильнике. При малейшей возможности Анатолий старался просмотреть все электронные письма, ответить на требующие ответа, побывать на сайтах – информационных и дискуссионных, ознакомиться с новостями на главных телеканалах. Как он сам говорил: «Информация – мать интуиции». И на ее сбор тратил от четырех до шести часов в сутки. В оставшееся время – все остальное.

С 2008 по 2010 год Анатолий был издателем научно-исследовательского журнала «Идея Икс», специализирующегося на компьютерных технологиях. В 2010 и 2012 годах был участником предвыборных кампаний в городе своего детства, Одессе. Десятки раз дистанционно участвовал в самых разных региональных предвыборных кампаниях по всей России, но сам считал, что его главная работа не столько предвыборная, сколько работа публициста и политического консультанта по многим вопросам текущей политики. Именно потому вел на Рен-ТВ передачи «Реакцию Вассермана» и «Открытым текстом», а на радиостанции «Комсомольская правда» – ток-шоу «Беседка с Анатолием Вассерманом».

«Реакция» Вассермана. 2013 год

В январе 2016 года «национальное достояние» и гражданин Украины стал гражданином России. В новом статусе он поучаствовал в выборах как кандидат в депутаты по региональному списку столицы от «справедливороссов» в Государственную думу. По округу оказался вторым, его опередил «единоросс» Евгений Жарков.

Анатолий Вассерман на съезде «Справедливой России»

Вассерман не расстроился, поскольку считал, что для него всегда найдутся интересные задачи. По его словам, экономика и политика как ее концентрированное выражение достаточно просты для понимания ключевых закономерностей здравомыслящим человеком. Но вот когда дело доходит до взаимодействия этих закономерностей, бывает сложно определить цепь последствий и здесь уже будет работа для политического консультанта:

Приходится выбирать теорию, указывающую, что важнее, и совершенствовать ее по мере обнаружения расхождений между ее прогнозами и последующими событиями. Мне чаще всего удается находить правильные прогнозы, значит, и теорию я развиваю в разумном направлении. Поэтому ко мне обращаются за разъяснениями.

Писатель и библиофил

Как и прежде, у Анатолия Вассермана в доме несметное количество книг, которые он начал собирать еще в детстве, продолжая семейную традицию. Помимо того, публицист с 2010 года начал и писательскую деятельность. Дебютом на этом поприще стала книга «Россия, включая Украину: Единство или гибель». Почти следом появляются «Хронические комментарии к российской истории» и «Скелеты в шкафу истории».

Анатолий Вассерман на презентации своей книги

Вместе с братом Владимиром, которого Анатолий считает гораздо умнее себя, написал «Прогулки по умным местам. Кое-что за Одессу» и несколько других книг, отличающихся легким стилем, ироничным юмором и подлинной любовью к обеим родинам – Украине и России. В библиографии братьев есть также книги для повышения интеллекта, развивающие энциклопедии, путеводители в виде увлекательных рассказов.

Сам себе стилист

Лишь ленивый не поинтересовался, что носит Вассерман в своей знаменитой жилетке и почему он вообще в ней ходит. А все дело в том, что в один из жизненных периодов Анатолию пришлось работать на свеклосахарных заводах, и бывали случаи, когда он безвылазно сидел в машинном зале по двое-трое суток. И тогда он понял, скольких необходимых ему вещей не хватает под рукой. В 1986 году он самостоятельно сшил первую свою жилетку с множеством карманов, в каждом из которых разместились все, по его мнению, необходимые вещи.

Знаменитая жилетка Анатолия Вассермана

В их числе – зарядные устройства, сетки, сумки, специальный нож с шипом – приспособление для спасения людей, попавших в ДТП. Ударом шипа при аварии можно быстро расколоть стекло автомобиля. Анатолий носит его при себе как коллекционный предмет, но ему нравится при этом думать, что если (не дай бог, конечно), случится беда, он сможет помочь людям. Позже Вассерман стал заказывать жилетки, а затем и брюки, спроектированные им самим в фирме «Спецодежда». Вес жилета раньше составлял 7 кг, но с возрастом эрудит облегчил нагрузку.

Личная жизнь Анатолия Вассермана

Анатолий Вассерман – девственник поневоле. Как не единожды признавался он сам, еще в студенческие годы эрудит дал обет целибата и соблюдает его по сей день. Полное отсутствие практики Анатолий компенсировал углубленным изучением теории. В его жилище, помимо множества книг по оружию, имеется изрядная коллекция эротических изданий, которые он начал собирать еще в советское время и время от времени ее пополняет.

Анатолий Вассерман девственник

Тем не менее, в одной из передач про асексуалов, куда Анатолия пригласили, как он иронично сообщал, «в качестве экспоната», он предупредил организаторов, что если хоть кто-то заикнется о нем как о положительном примере отказа от половой жизни, то он не поленится и собственноручно «набьет морду» тому гражданину:

У меня стандартное поздравление на свадьбах: «Поздравляю молодоженов, что не повторили мою ошибку», – сказал Вассерман в одном из интервью.

Несмотря на обет безбрачия, который Анатолий по прошествии лет назвал глупостью, дорого ему обошедшейся и не принесший очевидной пользы, он неоднократно заявлял, что ни жениться ради продолжения рода, ни воспользоваться услугами суррогатной матери ему в голову не приходило. Тем более что его «умный на самом деле, а не как я, распиаренный» брат уже явил миру наследницу рода Вассерманов. Племянницей своей Анатолий очень гордится.

Анатолий Вассерман сейчас

В 2019 году вновь проявился юмористический дар главного интеллектуала страны. Он согласился на съемки в клипе «Танцуй под Бузову» и даже изобразил несколько оригинальных па в ролике Ольги Бузовой в компании трех прелестниц.

Анатолий Вассерман в клипе Бузовой

Анатолий Вассерман был ведущим YouTube-шоу «Вынос мозга». В сюрреалистичных, нарочито нелепых декорациях он, стоя за штурвалом, задавал каверзные вопросы гостям студии – молодежным кумирам вроде рэперов (Паши Техника, Thrill Pill, Скруджи) и блогеров (Ильи Варламова, Lizzkи и пр.). Вассерман озвучивал невероятные факты, а его собеседникам надо было угадать, правда это или нет. Если гость ошибался, Анатолий выстреливал ему в лицо из пушки. Но шоу продержалось около года, и если первый выпуск собрал более миллиона просмотров, впоследствии количество зрителей упало.

Кадр из шоу «Вынос мозга» с Вассерманом

Не оставляет Вассермана надежда на появление телепередачи о военном деле по его проекту. Также Анатолий выезжает из Москвы, чтобы проводить лекции в других городах. После послания президента Владимира Путина Федеральному собранию в январе 2020 года Вассерман не медля выступил с аналитическим прогнозом в программе «Открытым текстом».

Вассерман об отставке Правительства в 2020

Недопустимое название — Викисловарь —

Содержание

Эрудит (игра) — это… Что такое Эрудит (игра)?

Скрэббл
Игра Скрэббл
Количество игроков	2-4
Диапазон возрастов	8+
Время установки	1 минута
Длительность партии	60 минут
Сложность правил	Простые
Уровень стратегии	Низкая
Влияние случайности	Низкое
Необходимые навыки	Наблюдательность, знание языка

Скрэббл (англ. Scrabble — «рыться в поисках чего-либо») — настольная игра, в которую могут играть от 2 до 4 человек, выкладывая слова из имеющихся у них букв в поле размером 15 x 15. В русскоязычной среде известна под названием «Эрудит».

Правила

Игровое поле состоит из 15х15, то есть 225 квадратов, на которые участники игры выкладывают буквы, составляя тем самым слова. В начале игры каждый игрок получает 7 случайных букв (всего их в игре 100). На середину игрового поля выкладывается первое слово, затем следующий игрок может добавить слово «на пересечение» из своих букв. Слова выкладываются либо слева направо, либо сверху вниз.

Словарь

Разрешается использовать все слова приведенные в стандартном словаре языка за исключением слов пишущихся с прописных букв, сокращений, и слов, которые пишутся через апостроф или тире. В варианте «Скрэббл» можно использовать все падежи, склонения и времена.

В то же время в игре «Эрудит» согласно традициям русских лингвистических игр разрешено использовать только имена существительные нарицательные в именительном падеже единственного числа (либо множественного при отсутствии у слова формы единственного числа).

Запрещено использовать словарь для поиска слов. Словарь разрешен только в случае проверки на существование уже выложенного слова.

Игра

• В начале игры каждому дается по 7 фишек. За один ход можно выложить несколько слов. Каждое новое слово должно соприкасаться (иметь общую букву или буквы) с ранее выложенными словами. Слова читаются только по горизонтали слева направо и по вертикали сверху вниз.
• Первое выложенное слово должно проходить через центральную клетку.
• Если игрок не хочет или не может выложить ни одного слова, — он имеет право поменять любое количество своих букв, пропустив при этом ход.
• Любая последовательность букв по горизонтали и вертикали должна являться словом. Т.е. в игре не допускается появление на поле случайных буквосочетаний, не представляющих собою слов, соответствующих вышеприведенным критериям.
• После каждого хода необходимо добрать новых букв до 7.
• Если за ход игрок использовал все 7 косточек, то ему начисляются дополнительные 50 очков.

Подсчет очков и бонусы

Каждой букве присвоено некоторое количество очков от 1 до 10. Некоторые квадраты на доске раскрашены в разные цвета. Количество очков, получаемых игроком за выложенное слово, подсчитывается следующим образом:

• если квадрат под буквой бесцветен, добавляется количество очков, написанное на букве
• если квадрат голубой, количество очков буквы умножается на 2
• если квадрат розовый, количество очков всего слова умножается на 2
• если квадрат синий, количество очков буквы умножается на 3
• если квадрат красный, количество очков всего слова умножается на 3

Если слово пересекает и красную и синюю клетки, то в удвоении (утроении) очков слова учитывается удвоение (утроение) очков букв.

Пустышка (джокер, «звёздочка»)

Также, в наборе косточек присутствует несколько пустых фишек (в версии «Эрудит» — звёздочек). Такая фишка может быть использована как любая буква на выбор игрока. Например, игрок может выставить слово «ТЕ*ЕФОН», где роль буквы «Л» будет играть пустышка.

Правила подсчета очков и использования пустышек могут отличаться и игрокам следует заранее договориться о нюансах.

Ниже приведены возможные варианты правил.

Подсчет очков за пустышку:

• Пустышка всегда имеет 0 очков (классические правила Scrabble).
• Пустышка приносит столько очков, сколько бы принесла буква, роль которой она играет.

Повторное использование пустышек:

• После выкладывания на поле, пустышка считается сыгранной и так и остается на этом месте до конца партии (классические правила Scrabble).
• Если один игрок выложил слово «ТЕ*ЕФОН», то затем, любой игрок, имея у себя букву «Л», может заменить ее на пустышку и забрать ее себе. Как правило, действует дополнительное правило, обязывающее в таком случае использовать (выложить) забранную с поля пустышку этим же ходом, т.е. когда нельзя брать ее себе «про запас».

История

Игра была изобретена в 1938 году архитектором Альфредом Баттсом. В США и многих странах Европы до сих пор проводятся регулярные чемпионаты по Скрэбблу.

Различия между «Эрудит» и «Скрэббл»

Параметр	«Скрэббл»	«Эрудит»
«универсальная» фишка	пустышка	звездочка
цвета бонус-клеток	голубой, синий, розовый, красный	зеленый, голубой, желтый, красный
различная стоимость букв	Ю:8	Ю:10
буква «Ё»	присутствует	отсутствует
количество фишек	104	129

Модификации игры

Ссылки

Wikimedia Foundation. 2010.

Вики ЦДО

Добро пожаловать на ВикиСтавЦДО!

Cайт поддерживается Центром дистанционного обучения и информационных технологий
ГБУ ДПО «Ставропольский краевой институт развития образования, повышения квалификации и переподготовки работников образования»

Уважаемые коллеги! Приглашаем Вас вступать в сетевые сообщества педагогических работников Ставропольского края. Сетевые сообщества педагогов, не знающие границ и расстояний, легко решают ряд важных для педагога задач. Участие в профессиональных сетевых объединениях позволит Вам, живущим в разных уголках Ставропольского края общаться друг с другом, решать профессиональные вопросы, реализовать себя и повышать свой профессиональный уровень.

Цель сетевых сообществ: объединение педагогических работников по их профессиональным интересам и создание единого информационно-методического пространства для педагогов края. Задачи Сообществ: — обеспечение методической поддержки массового внедрения (цифровых) образовательных ресурсов и инструментов в педагогическую практику; — организация информационно-методической поддержки и профессиональной взаимопомощи; — создание базы данных по программным продуктам учебного назначения и опыту их применения на уроках и во внеурочной деятельности; — обмен опытом в области применения новых педагогических технологий; — организация формального и неформального общения по профессиональным проблемам; — распространение педагогических практик и др.

ОПЫТ РЕГИОНОВ

Летописи.ру Общенациональный образовательный проект с международным участием Открытый класс Сетевые образовательные сообщества СоцОбраз Сетевое социально-педагогическое сообщество ХабаВики Площадка учителей, методистов и школьников Хабаровского края Wiki.SibiriaDa Портал Wiki.SibiriaDa Wiki-Vladimir Ресурс Владимирского института повышения квалификации работников образования АвачаВики Интернет-площадка для поддержки творчества учителей, методистов, студентов и школьников Камчатского края

ПримWiki Площадка для методистов, учителей и школьников Приморского края ОренВики. ru Единая образовательная среда преподавателей, методистов и школьников Оренбурга и Оренбургской области ГБУ «Региональный центр развития образования Оренбургской области» Тамбов-Вики WikiWiki Тамбовского областного государственного образовательного автономного учреждения дополнительного профессионального образования «Институт повышения квалификации работников образования» Псковская региональная образовательная Wiki Сайт педагогического сообщества Псковской области СарВики Вики-сайт Саратовского ИПК и ПРО Иркутская Wiki Сообщество учащихся, студентов и педагогов Иркутской области

Новый Спортивный Эрудит.

Завершен. : Спортивный эрудит

[font=Verdana]Пришло время подвести итоги 3-го тура.
На сей раз все оказалось проще, чем в прошлый раз.
Тем не менее…
Правильные ответы.

1 — Александр Анатольевич Кузнецов, прославленный российский велотренер, воспитавший немало классных гонщиков.
Самыми знаменитыми учениками Александра Кузнецова являются Вячеслав Екимов , Михаил Игнатьев , Евгений Берзин , Дмитрий Нелюбин , Александр Краснов , Виктор Манаков , а также его собственная жена — шестикратная чемпионка мира в трековом спринте Галина Царева и сын — Николай Кузнецов .
Отец Светланы Кузнецовой, известной теннисистки.

2 — Анна Владимировна Бессонова, Заслуженный мастер спорта Украины. Трехкратная чемпионка Европы, четырехкратная чемпионка мира, обладательница Кубка Мира, абсолютная чемпионка мира 2007 года. Обладательница бронзовой медали на Олимпиаде 2004 года в Афинах. Бронзовая призерка XXIX Олимпийских игр в Пекине 2008 года.
Родилась в семье футболиста Владимира Бессонова и гимнастки Виктории Серых.

3 — Светлана Александровна Кузнецова — российская теннисистка, заслуженный мастер спорта России. Чаще всех россиян играла в финалах турниров Большого шлема во всех разрядах — 11 раз (4 в одиночном разряде и 7 — в парном). Трехкратная победительница Кубка Федерации в составе сборной России. Светлана стала третьей российской теннисисткой, выигравшей турнир Большого шлема в одиночном разряде. В возрасте 19 лет в 2004 году она стала победительницей Открытого чемпионата США. В 2009 году выиграла Открытый чемпионат Франции.
Дочь Александра Анатольевича Кузнецова и Галины Царевой.

4 — Татьяна Анатольевна Тарасова — выдающийся советский и российский тренер по фигурному катанию. Заслуженный тренер СССР .
Она подготовила больше будущих чемпионов мира и Олимпийских игр, чем какой-либо другой тренер в истории.Среди её учеников были Ирина Роднина, Алексей Ягудин, Илья Кулик, Наталья Бестемьянова, Марина Климова, Саша Коэн, Алиса Дрей, Джонни Вейр, Сидзука Аракава, Оксана Грищук, Барбара Фузар-Поли и многие другие.
Дочь не менее выдающегося тренера Анатолия Тарасова.

5 — Ольга Сергеевна Забелинская, российская велогонщица, Двукратная чемпионка мира среди юниорок на треке (1997). Чемпионка Европы на шоссе (2002). Бронзовый призер этапа Джиро-д’Италия (2010).
Отец Забелинской – олимпийский чемпион 1980 года по велоспорту Сергей Сухорученков. Однако, Ольга родилась вне брака, и познакомилась с отцом уже во взрослом возрасте.
Кстати, oтец сына Забелинской Богдана – известный велогонщик, чемпион России Сергей Иванов.

6 — Марина Вячеславовна Анисина — российская и французская фигуристка, завоевавшая в паре с Гвендалем Пейзера титулы чемпионки мира в 2000 году и Олимпийской чемпионки в 2002 году в танцах на льду.
Марина Анисина родилась в семье известной фигуристки Ирины Черняевой и хоккеиста Вячеслава Анисина.

7 — Вячеслав Михайлович Анисин — советский хоккеист, заслуженный мастер спорта СССР, участник легендарной суперсерии СССР — Канада 1972 года. Многократный чемпион мира, Европы и СССР.
Выступал за московские клубы ЦСКА, «Спартак» и «Крылья Советов», а также за ленинградский СКА.

8 — Владимир Васильевич Бессонов — советский футболист, полузащитник, позднее украинский футбольный тренер. Заслуженный мастер спорта СССР. С 1976 по 1990 год играл в киевском «Динамо».В 1980 играл за олимпийскую сборную СССР на футбольном турнире Олимпиады-80, провел 6 матчей и забил 1 гол.
В сборной СССР — 79 матчей, забил 4 гола.
Отец гимнастки Анны Бессоновой.

9 — Анатолий Владимирович Тарасов — советский хоккеист, футболист и тренер по этим видам спорта. Заслуженный мастер спорта СССР . Заслуженный тренер СССР
Согласно «Британской энциклопедии», Тарасов — «отец российского хоккея», сделавший СССР «доминирующей силой в международных соревнованиях».
Отец тренера по фигурному катанию Татьяны Тарасовой.

10 — Паоло Чезаре Мальдини — итальянский футболист, многолетний капитан сборной Италии и «Милана». Играл на позиции центрального и левого защитника. Сын знаменитого футболиста Чезаре Мальдини. Культовый футболист для болельщиков «Милана».
Всю свою футбольную карьеру провёл в «Милане», за который сыграл 902 официальных матча.
Провел 126 матчей в составе сборной Италии.
Паоло Мальдини является абсолютным рекордсменом по количеству сыгранных матчей в итальянской серии «А» (647 матчей).

11 — Сергей Николаевич Сухорученков — советский велогонщик, олимпийский чемпион в групповой шоссейной гонке на летних Олимпийских играх 1980 года. Заслуженный мастер спорта СССР .
Многократный чемпион СССР в 1979—1983 гг. Дважды (1979 и 1984) побеждал в индивидуальном зачёте на Велогонке Мира, в командном зачёте — в 1979, 1981, 1984.
В 1979, 1980 и 1981 годах признавался французской газетой «Экип» сильнейшим велогонщиком мира среди любителей.
Отец Ольги Забелинской, и еще 5!!!!! сыновей, к большому спорту, правда, отношения не имеющих.

12 — Чезаре Мальдини — знаменитый итальянский футболист и тренер, был столпом обороны сборной Италии и «Милана» образца 60-х годов. Играл на позиции защитника.
Пять лет проработал вторым тренером «Милана». Затем был одним из ассистентов «комиссарио текнико» (так в Италии называют главного тренера). В частности, в золотом для итальянской команды 1982 году помогал Энцо Беарзоту. Затем трудился в олимпийской и молодежной сборной Италии (U-21), трижды привел её к званию чемпиона Европы.
В декабре 1996 года Чезаре Мальдини возглавил сборную Италии. После провала на Чемпионате мира 1998 года Мальдини вынужден был подать в отставку.
Отец знаменитого футболиста Паоло Мальдини.

Как почти все отметили, темой задания была тема «Отцы и дети».
1; 3 — Александр и Светлана Кузнецовы
2; 8 — Анна и Владимир Бессоновы
4; 9 — Татьяна и Анатолий Тарасовы
5; 11 — Ольга Забелинская и Сергей Сухорученков
6; 7 — Марина и Вячеслав Анисины
10; 12 — Паоло и Чезаре Мальдини.

Есть одно маленькое замечание по поводу правильности написания фамилии Ольги Забелинской
Несколько участников назвали ее Зебелинской. Я долго не могла понять, откуда идет эта ошибка.
Обнаружила ее вчера. Увы, не раз уже отмечалось, что Википедия грешит неточностями. Поэтому то, что написано в Википедии, стоит проверять еще и с помощью других источников.
Но поскольку понятно, что все имели в виду одну и ту же спортсменку, я приняла все ответы как правильные.

Итак, на все вопросы ответили
samuist
GAN
sedoy22
Rom4ig
7Andreas7
хмырь
WERT
Igor07
Sweeter
Jimm
Fraskini
Тайлер
Bosfan
Nadia
Mihal101
AVerTV

Второй раз подряд расторопнее всех стал samuist
По правилам конкурса он объявляется победителем 3-го тура и получает вторую звезду и поздравления.

И статистика.
В 3-м туре приняли участие 18 человек (пока рекордное количество играющих)
12 правильных ответов получены от 16 участников
10 — от 1 (Виталий, который с Подола, не верю, что ты не знал. Просто, видимо, времени не хватило разобраться с последней парой).
5 ответов дал тоже 1 участник.
На дополнительный вопрос (то бишь разгадали принцип составления пар) ответили 17 участников.

Количество упоминаний.
1. Александр Кузнецов -18
2. Анна Бессонова — 17
3. Светлана Кузнецова -18
4. Татьяна Тарасова — 18
5. Ольга Забелинская — 17
6. Марина Анисина — 17
7. Вячеслав Анисин — 17
8. Владимир Бессонов 17
9. Анатолий Тарасов -17
10. Паоло Мальдини — 18
11. Сергей Сухорученков — 16
12. Чезаре Мальдини — 17

Спасибо всем за участие. Радостно, что, практически, все знают не только современных спортсменов, но и героев спорта прошлых лет. [/font]

Список эрудитов — EverybodyWiki Bios & Wiki

Имя	Родился	Национальность	Искусство				Фундаментальные науки			Прикладные науки
			Изобразительное искусство	Литературное искусство	Исполнительское искусство и кино	Прикладное искусство	Формальные науки	Естественные науки	Социальные науки	Архитектура	Образование	Инжиниринг	Здоровье	Менеджмент	Другое
Аристотель	-384	Македонская империя (греческий)		Теория искусств и критика			Логика	Физика, Астрономия, Биология, Геология, Психология	Этика, философия, экономика, политика		Учитель философии	Классическая механика, Оптика		Теория правительства
Птолемей	100	Египет, Римская империя (греческий)		Поэзия	Теория музыки		Математика	Астрономия, Астрология, География	Философия			Оптика
Авиценна	980	Империя Саманидов Зиярид Табаристан Buyid Persia (персидский)		Поэзия			Логика	Физика, Химия, Астрономия, Астрология	Философия		Учитель		Медицинская энциклопедия
Леонардо да Винчи	1452	Республика Флоренция (итальянский)	Картины, рисунки, фрески, скульптура	Поэзия	Музыка (Лира)		Математика	Физика, Анатомия, Физиология	Теория искусства	Архитектура, Градостроительство, Мосты	Учитель рисования	Вертолет, Летающая машина, Подводная лодка, Оптика, Гидродинамика, Музыкальные инструменты, Механический рыцарь, Гидравлические насосы, Реверсивные кривошипные механизмы, Снаряды с ребристыми минометами, Парашют, Паровая пушка, Самоходная машина	Кулинарный
Готфрид Вильгельм Лейбниц	1646	Электорат Саксонии, Священная Римская империя (немецкий)		Поэзия		Теория игр	Математика, логика	Физика, космология, эмбриология, палеонтология	Филология, философия, юриспруденция, синофил, экономика, психология		Программа медицинского обучения	Механика, Винты с ветровым приводом, Водяные насосы, Горные машины, Гидравлические прессы, Лампы, Подводная лодка, Часы, Паровой двигатель	Медицинское письмо	Дипломатия
Михаил Ломоносов	1711	Царство Русское (русский)	Мозаика	Поэзия				Физика, география, химия, геология	История, Филология		Профессор	Зрительная труба отражающая

Блог эрудита | Массовые совместные математические проекты

Мы еще не достигли отметки в 100 комментариев ко второму сообщению в блоге Polymath 12, но похоже, что сейчас подходящий момент для подведения итогов. Проект частично утратил свою первоначальную динамику, возможно, из-за того, что в жизни основных участников вторглись другие приоритеты (я знаю, что это верно и для меня). Однако я пока не хочу выключать свет, потому что не верю, что мы на самом деле застряли. Позвольте мне воспользоваться этой возможностью, чтобы описать некоторые из потенциальных клиентов, которые я считаю наиболее многообещающими.

Онлайн-версия гипотезы

Для обычных матроидов онлайн-версия гипотезы Роты об основаниях неверна, но все же интересно спросить, сколько оснований достижимо.На мой взгляд, одним из самых приятных моментов в выпуске Polymath 12 был частичный ответ на этот вопрос: он находится где-то между n /3 + c и n /2 + c . Есть надежда, что этот пробел можно будет ликвидировать. Если удастся устранить этот пробел, то, на мой взгляд, это была бы короткая статья, которую можно было бы опубликовать. Кстати, если статью публикует Polymath 12, какой псевдоним следует использовать? Я знаю, что для первого проекта использовался D. H.J. Polymath, но, возможно, R.B.C. Polymath имеет больше смысла?

Графические матроиды

Было высказано предположение, что графические матроиды могут быть более сговорчивым частным случаем. Мне сначала не сразу было понятно почему, но теперь я понимаю лучше. В частности, графические матроиды без K ₄ minor являются последовательно-параллельными и, следовательно, имеют строгий базовый заказ и, следовательно, удовлетворяют основной гипотезе Роты. Таким образом, в некотором смысле K ₄ — это , только препятствие для основной гипотезы Роты для графических матроидов, тогда как аналогичное утверждение для матроидов в целом не выполняется.

В одной из своих статей я показал, грубо говоря, что если можно доказать версию n × 2 базовой гипотезы Роты, то этот факт можно превратить в доказательство полной гипотезы. Конечно, версия n × 2 в целом неверна, но я верю, что полное понимание того, что может произойти всего в двух столбцах, даст существенное понимание всей гипотезы. Один вопрос, который я поднял, заключался в том, может ли любое расположение ребер n × 2 дать два столбца, которые являются основаниями, если мы вытащим не более n /3 ребер.Возможно, это несколько неуклюжий вопрос, но он пытается ответить на вопрос, существуют ли какие-либо контрпримеры n × 2, которые не являются просто несвязным объединением копий K ₄ , которые были расширены с помощью “ разжимать »некоторые края. Если мы сможем классифицировать все контрпримеры n × 2, то я думаю, что это будет большим шагом к доказательству полной гипотезы для графических матроидов.

Конечно, это не единственный способ справиться с графическими матроидами.Главное, что я думаю, есть потенциал для серьезного прогресса в этом частном случае.

Вычислительные исследования

Я упомянул неопубликованную рукопись Майкла Ченга, в которой сообщается, что случай n = 4 основной гипотезы Роты верен для всех матроидов. Я считаю, что это впечатляющее вычисление, и я думаю, что оно заслуживает независимой проверки.

На мой взгляд, поиск контрпримеров 5 × 2 к основной гипотезе Роты также может пролить свет.Гордон Ройл предоставил ссылку на базу данных всех девятиэлементных матроидов, которая должна быть полезной. Люк Пебоди начал свой путь по этому пути, но, насколько мне известно, еще не завершил вычисления.

Матроиды с строго базовым заказом

В 1995 году Марсель Вильд доказал следующий результат («лемма 6»): Пусть будет матроид на -элементном множестве, который является несвязным объединением независимых множеств размера. Предположим, что существует другой матроид на том же самом наборе земли со следующими свойствами:

(1) является строго базовым для заказа.

(2) для всех, где — функция ранга.

(3) Все схемы удовлетворения остаются зависимыми.

Тогда есть сетка, в которой есть я-я строка, а столбцы в ней независимы.

Уайлд получил несколько частичных результатов как следствие леммы 6. Сколько миль мы можем извлечь из этого? Всегда ли найдется подходящий для графических матроидов?

Варианты и связанные с ними предположения

Я менее оптимистичен в отношении того, что это приведет к прогрессу в отношении самой основной гипотезы Роты, но, возможно, я ошибаюсь.Гил Калаи сделал несколько предложений:

1. Рассмотрим d + 1 (аффинно независимый) подмножество размера d + 1 таких, что начало координат принадлежит внутренней части выпуклой оболочки каждого набора. Можно ли найти наборы d + 1 размером d + 1, такие, что каждый набор представляет собой набор радуги, а внутренняя часть выпуклых корпусов всех этих наборов имеет общую точку?
2. Гипотеза о широком разбиении или ее обобщение на произвольные разбиения.
3. Если у нас есть наборы B ₁ ,…, B _n (не обязательно основания), которые не могут быть расположены так, чтобы все столбцы n были основаниями, то всегда можно найти несвязанные n + 1 набор C ₁ ,…, C _{n +1} , так что каждый набор содержит не более одного элемента от каждого B _j и пересечение всех линейных пролетов C _i нетривиально? (Признаюсь, я до сих пор не понимаю, почему мы должны ожидать, что это правда. )

Павел Патак представил лемму из одной из своих статей, которая может оказаться полезной. Пусть M будет матроидом ранга r и пусть S будет последовательностью из kr элементов из M , разделенных на r подпоследовательностей, каждая из которых имеет длину не более k . Тогда любая наибольшая независимая подпоследовательность радуги S является основой M тогда и только тогда, когда не существует целого числа s r и набора s + 1 цветовых классов, так что объединение эти цветовые классы имеют ранг и .

В другом направлении есть теоретико-графические гипотезы, такие как гипотеза Бруальди – Холлингсворта: если полный граф K _{2 m} (для m ≥ 3) раскрашен ребрами таким образом, что каждый цветовой класс является идеальным соответствием, тогда существует разложение ребер на м непересекающихся по краям радуги остовных деревьев.

Замечания к предыдущему сообщению в блоге

Наконец, позвольте мне сделать несколько замечаний о направлениях исследований, которые были предложены в моем предыдущем сообщении в блоге Polymath 12.Сначала я оптимистично смотрел на матроиды с немалыми схемами, и я все еще думаю, что о них стоит подумать, но теперь я более пессимистичен, что мы можем извлечь большую пользу из простого обобщения методов Гилена и Хамфриса по причинам, которые можно найти прочитав комментарии. Точно так же я более пессимистичен сейчас, когда алгебро-геометрический подход даст что угодно, поскольку быть базисом — это открытое, а не закрытое условие.

Другие зацепки в этом сообщении в блоге не особо обсуждались, и я думаю, что на них все еще стоит взглянуть.В частности, эта старая резервная гипотеза Алона – Тарси может по-прежнему допускать более частичные результаты. Предложение Ребекки Стоунс о том, что, возможно, L _n ^четное — L _n ^{нечетное} ≢ 0 (мод. p ), когда p = 2 n + 1 простое, все еще выглядит мне как хорошая идея, и я не думаю, что многие люди всерьез задумывались об этом. Также я согласен с Дэвидом Глинном в том, что большему количеству людей следует изучить недавнюю статью Карлоса Гамаса о гипотезе Алон-Тарси.

Определение

в кембриджском словаре английского языка

В его состав входило несколько профессиональных астрономов, но было много врачей, литераторов, дипломатов, студентов, эрудитов и джентльменов с различным образованием. Мы думали, что он превзошел все свои способности, и ничего не знали о его натуре эрудита .

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

Еще примеры Меньше примеров

Читатели закончат книгу вполне удовлетворенными, и, если они не являются настоящими историческими эрудитами, гораздо лучше информированными, чем они были до того, как начали. Однако эрудиты больше не пишут о других эрудитах, а специалисты о эрудитах. Что-то вроде эрудита , он наладил связи между дисциплинами и отстаивал идею о том, что фотосинтез был заимствован бактериями, которые возникли с морского дна и впоследствии колонизировали сушу.Подобная работа не может быть написана или рецензирована одним человеком, поскольку необходимая эрудиция сегодня не может быть найдена даже у одного эрудита . Фуллер считает себя эрудитом , говорящим об огромном диапазоне интеллектуальных и политических тенденций двадцатого века. Вы обнаружите, что эти восемь мест должны быть заполнены эрудитами, если вы хотите, чтобы это вообще работало. Одна из наших целей в 21 веке должна заключаться в том, чтобы попрощаться со школьником-специалистом и поприветствовать школьника , эрудита .Чтобы охватить поднятые темы, нужно быть чем-то вроде эрудита . Он должен быть настоящим эрудитом .Я отдаю ему должное за то, что он инициировал дебаты и предоставил нам всю информацию, а также за то, что он настоящий эрудит — инженер, который может исправить свои собственные герундий. Он был признан величайшим эрудитом своего возраста. Из

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Он был эрудитом и проводил исследования в области геологии, минералогии, ботаники, химии, этнографии, петрологии и карстологии.Из

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Он был великим эрудитом , музыкантом, астрономом, поэтом, изобретателем термина география и математиком. Из

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.

Проект «Полимат»: объем участия

Как я упоминал ранее, в течение последних семи недель математик Тим Гауэрс проводил замечательный эксперимент в , как выполняется математика , проект, который он назвал проектом Polymath3.Используя принципы, аналогичные тем, которые используются в проектах программирования с открытым исходным кодом, он использовал блоги и вики для организации открытого математического сотрудничества, пытающегося найти новое доказательство важной математической теоремы, известной как теорема Хейлса-Джуэтта (DHJ) о плотности. Проблема была серьезной. Гауэрс, опытный профессиональный математик, первоначально думал, что шансы на успех «существенно меньше 100%», даже принимая довольно скромный критерий успеха.

На прошлой неделе Гауэрс объявил, что проблема «вероятно решена».Фактически, если результаты подтвердятся, проект превзойдет ожидания. Первоначальная цель состояла в том, чтобы найти новое доказательство важного частного случая теоремы DHJ с использованием особого подхода, предложенного Гауэрсом (или объяснить, почему этот подход не удался). Эта цель со временем расширилась, и в рамках проекта, похоже, было найдено новое доказательство полной теоремы с использованием подхода, отличного от первоначально предложенного Гауэрсом. Выполняется запись. Вдохновленный работой Polymath3, математик Тим Остин выпустил препринт, в котором утверждается, что еще одно доказательство DHJ, и цитируется Polymath3 как решающий для его работы.

Размах участия в проекте впечатляет. В блоге Гауэрса и в блоге Терри Тао, еще одного математика, сыгравшего ведущую роль в этом проекте, написано более 1000 математических комментариев. Вики Polymath насчитывает около 59 страниц с контентом, с 11 зарегистрированными участниками и большим количеством анонимных участников. Это уже замечательный ресурс по теореме Хейлса-Джеветта о плотности и смежным темам. График проекта показывает заметный математический вклад, сделанный на сегодняшний день 23 участниками.Это было сделано за семь недель.

Первоначальная надежда заключалась в том, что проект станет «массовым сотрудничеством». Предположим, мы возьмем указанное выше число (23) как репрезентативное для числа людей, внесших заметный математический вклад, имея в виду, что существуют очевидные существенные ограничения на использование временной шкалы таким образом. (Временная шкала содержит некоторые указатели на заметные общие комментарии, которые я не включил в этот подсчет.) Конечно, 23 человека — это очень большое число для математического сотрудничества — через несколько дней после начала проекта Тим Гауэрс заметил, что «это процесс является обычным исследованием, как вождение автомобиля — это толкание автомобиля », но он также сильно отстает от массового сотрудничества, такого как Linux и Wikipedia. Гауэрс заметил, что «я думал, что будут десятки участников, но вместо этого число сократилось до нескольких, всех из которых я знал лично».

Эти числа приобретают другой оттенок, однако, если вы заметите, что количество вовлеченных людей выгодно отличается даже от очень успешного сотрудничества с открытым исходным кодом: при семинедельной отметке . Через 7 недель после создания Википедии в ней было примерно 150 статей. Это значительно больше, чем вики Polymath3, но имейте в виду, что (а) вики Polymath3 — это лишь небольшая часть всего проекта; и (б) Я сомневаюсь, что кто-то не согласится с тем, что среднее качество вики Polymath3 значительно выше.Точно так же, хотя Linux сейчас получил пожертвования от нескольких тысяч человек, на создание этого сообщества ушли годы. Спустя 6 месяцев после того, как Линус Торвальдс впервые объявил о Linux, в списке рассылки Linux-активистов было 196 человек, но большинство из них просто смотрели. Многие даже не установили Linux (в то время сложная операция), а тем более внесли существенный вклад. Готов поспорить, что за Polymath3 подписано более 196 человек.

Многое можно сказать о масштабировании будущих проектов.Я считаю, что это можно сделать и что есть потенциально существенные дополнительные преимущества. А пока сделаю одно замечание. Долгоживущее сотрудничество с открытым исходным кодом иногда начинается с узконаправленных целей, но обычно со временем они расширяются и становятся более открытыми, позволяя сообществу участников продолжать расти с течением времени. Это, безусловно, верно в отношении Linux, цель которого — создание ядра операционной системы — чрезвычайно широка. В то же время эта широкая цель естественным образом порождает множество целенаправленных и до некоторой степени независимых проблем, которые могут быть решены сообществом разработчиков параллельно.Возможно, на этом этапе можно естественным образом расширить цели Polymath3, но это кажется интересной задачей — в то же время сохранить острую проблемно-ориентированную направленность, которая характеризовала сотрудничество.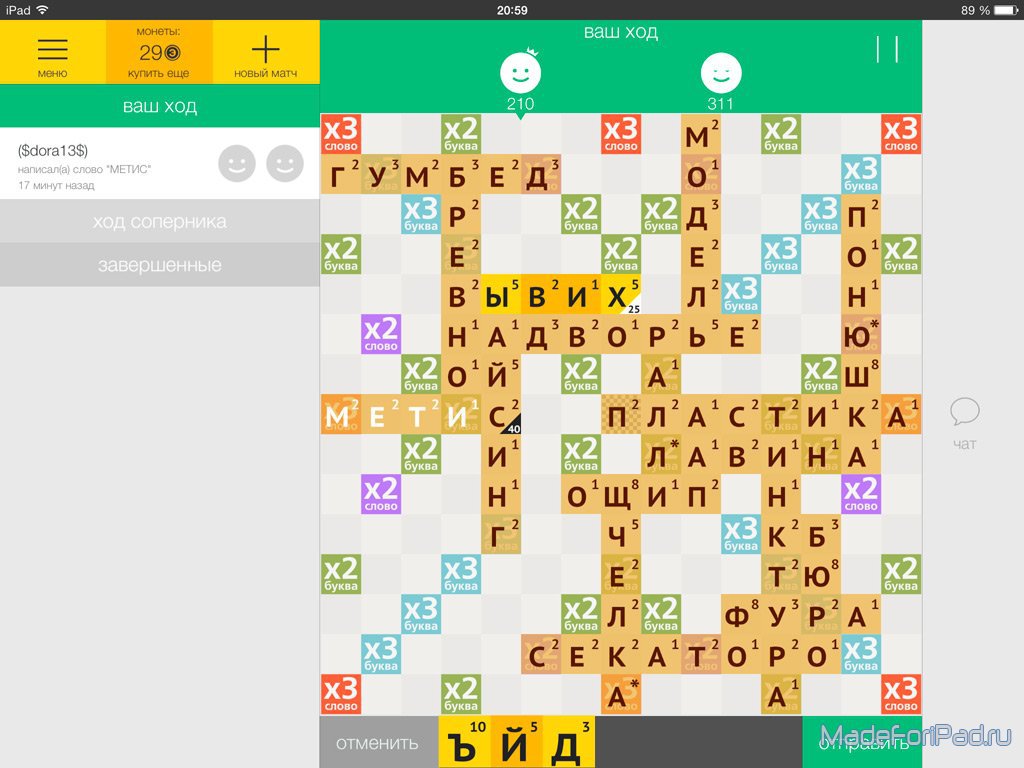

Математическое доказательство размером с Википедию слишком велико для проверки людьми

Джейкоб Арон

Если ни один человек не может проверить доказательство теоремы, действительно ли это считается математикой? Это интригующий вопрос, поднятый последними компьютерными доказательствами.Он такой же большой, как и все содержимое Википедии, поэтому маловероятно, что он когда-либо будет проверен человеком.

«Возможно, мы каким-то образом попали в утверждения, которые, по сути, являются нечеловеческой математикой», — говорит Алексей Лисица из Ливерпульского университета, Великобритания, который вместе с коллегой Борисом Коневым придумал доказательство.

Доказательство — важный шаг к решению давней загадки, известной как проблема несоответствия Эрдеша. Она была предложена в 1930-х годах венгерским математиком Полем Эрдешем, который предложил за ее решение & долларов США.

Представьте себе случайную бесконечную последовательность чисел, содержащую только +1 и -1. Эрдош был очарован степенью, в которой такие последовательности содержат внутренние закономерности. Один из способов измерить это — отрезать бесконечную последовательность в определенной точке, а затем создать конечные подпоследовательности в этой части последовательности, например, рассмотреть только каждое третье число или каждое четвертое.

Реклама

Сложение чисел в подпоследовательности дает число, называемое несоответствием, которое действует как мера структуры подпоследовательности и, в свою очередь, бесконечной последовательности по сравнению с однородным идеалом.

Подтверждение размера из Википедии

Эрдеш думал, что для любой бесконечной последовательности всегда можно найти конечную подпоследовательность, суммирующую число, большее, чем любое выбранное вами, — но не смог этого доказать.

Относительно легко показать от руки, что при любом расположении 12 плюсов и минусов всегда есть подпоследовательность, сумма которой превышает 1. Это означает, что что-либо более длинное, включая любую бесконечную последовательность, также должно иметь расхождение в 1 или более. Но расширить этот метод, чтобы показать, что более высокие расхождения всегда должны существовать, сложно, так как количество возможных подпоследовательностей для быстрого тестирования выскакивает.

Теперь Конев и Лисица передвигали вещи на компьютере. Они показали, что бесконечная последовательность всегда будет иметь несоответствие больше 2. В этом случае отсечка была последовательностью длиной 1161, а не 12. На ее установление у компьютера ушло почти 6 часов и сгенерирован 13-гигабайтный файл с подробностями. работает.

Пара сравнивает это с размером Википедии, текст которой загружается на 10 гигабайт. Вероятно, это самое длинное доказательство, когда-либо существовавшее & col; оно затмевает другое широко известное доказательство, которое включает в себя 15 000 страниц вычислений.

Потребуются годы, чтобы проверить работу компьютера, а расширение метода для проверки еще более высоких расхождений может легко привести к доказательствам, которые просто слишком длинные, чтобы их могли проверить люди. Но это поднимает интересный философский вопрос, — говорит Лисица и Колон; действительно ли может быть принято доказательство, если его не читает ни один человек?

Нечеловеческая математика

Гил Калаи из Еврейского университета в Иерусалиме, Израиль, говорит, что проверка человеком не обязательна для того, чтобы доказательства были в силе.«Меня не беспокоит тот факт, что ни один математик-человек не может это проверить, потому что мы можем проверить это с помощью других компьютерных подходов», — говорит он. Если компьютерная программа, использующая другой метод, дает тот же результат, то доказательство, скорее всего, будет правильным.

Калаи был частью группы, которая в 2010 году решила поработать над этой проблемой как проект Polymath — упражнение, в котором математики используют блоги и вики-сайты для крупномасштабного сотрудничества. Запустив другое программное обеспечение, группе удалось протестировать последовательность длиной 1124 — близкую к пороговому значению, которое, как показали Конев и Лисица, теперь необходимо, — но сдались, когда программа не могла масштабироваться до более высоких чисел.

Однако, когда дело доходит до проблемы несоответствия Эрдеша, у людей все еще есть надежда. Гипотеза Эрдеша заключалась в том, что всегда можно найти несоответствие любого значения, в отличие от доказанных несоответствий 1 и 2. Программное обеспечение Лисицы работало в течение нескольких недель в попытке найти результат для расхождения 3. Но даже если последующие программы показывают, что все большие и большие расхождения существуют для любой бесконечной последовательности, компьютер не может проверить бесконечность всех чисел.

Вместо этого вполне вероятно, что компьютерные доказательства конкретных расхождений в конечном итоге позволят человеку обнаружить закономерность и придумать доказательство для всех чисел, — говорит Лисица. «Нерешенные проблемы подобны маякам; они ставят перед нами цели для наших способностей », — добавляет Калаи.

Ссылка & двоеточие; arxiv.org/abs/1402.2184

Предыдущее обучение: Математика 247B (анализ Фурье на уровне выпускников) S’20 Математика 254A (аналитическая теория чисел) F’19 Математика 255B (Несжимаемые уравнения Эйлера) W’19 Математика 254A (Математика 254A) Несжимаемые жидкости) F’18 Math 246C (Комплексный анализ) S’18 Math 245C (Реальный анализ) S’17 Math 246A (Комплексный анализ) F’16 Math 245C (Реальный анализ) S’16 Математика 275A (Вероятность) F’15 Математика 254A (Аналитическая теория простых чисел) W’15 Математика 245C (Реальный анализ) S’14 Математика 245B (Реальный анализ) W’14 Математика 245C ( Реальный анализ) S’13 Math 245B (Реальный анализ) W’13 Math 254B (Разложение по группам типа Ли) W’12 Math 254A (Пятая проблема Гильберта) F’11 Math 245C (Real Анализ) S’11 Math 245A (Реальный анализ) F’10 Math 254B (Анализ Фурье высшего порядка) S’10 Math 254A (Случайные матрицы) W’10 Math 245C (Реальный анализ выпускников) S’09 Math 245B (Реальный анализ выпускников) W’09 Math 285G (гипотеза Пуанкаре) S’08 Математика 254A (эргодическая теория) W’08

Предыдущее обучение: Математика 247B (последующий анализ Фурье) W’07 Математика 247A (последующий анализ Фурье) F’06 Математика Введение в PDE) S’06 Math 251A (Введение в PDE) W’06 Math 245C (Real Analysis) S’05 Math 33A (Linear Algebra) W’05 Math 245B (Real Analysis) W ‘ 05 Math 245A (Реальный анализ) F’04 Math 133 (Анализ Фурье) W’04 Math 245B (Реальный анализ) W’04 Maths 3228 (Комплексный анализ) S’03 Math 131BH ( Honors Real Analysis) S’03 Math 131AH (Honors Real Analysis) W’03 Math 254A (Аддитивная комбинаторика) W’03 Математика 115A (Линейная алгебра) F’02 Математика 254A (Частотно-временной анализ) W’01 Математика 199 (Решение проблем) S’00 Математика 121 (Введение в топологию) S’00 Математика 132 (Комплексный анализ) W’00 Math 254B (Restriction / Kakeya) S’99 Math 254A (Осциллирующие интегралы) W’99

Разное: Java-приложения 0 Диверсии Vitae Карьерный совет Написание совета

Поток DOI в реальном времени, цитируемый в Википедии

TL; DR

Смотрите в реальном времени поток цитируемых (и «не цитируемых!») DOI в статьях Википедии по всему миру: http: // goo. gl / 0AknMJ

Фон

В течение многих лет мы знали, что Википедия является основным источником ссылок на DOI Crossref, и около года назад мы подтвердили, что на самом деле Википедия является 8-м по величине ссылками DOI Crossref. Мы знаем, что люди тоже следят за DOI. И это несмотря на то, что в Википедии очень мало цитирований научной литературы даже с использованием DOI. Поэтому еще в августе мы решили создать программу послов Викимедиа. Целью программы было продвижение использования постоянных идентификаторов при цитировании и атрибуции в статьях Википедии.Мы могли бы сделать это посредством разъяснительной работы и разработки более совершенных инструментов, связанных с цитированием.

Помните, когда мы первоначально писали о наших экспериментах с кодом PLOS ALM и как он перешел в пилотную программу отслеживания событий DOI? В этих сообщениях мы упоминали, что одним из препятствий при сборе информации о событиях DOI является фактический процесс опроса сторонних API на предмет активности, связанной с миллионами DOI. Большинство сторон просто не захотят обрабатывать 100 000 вызовов API в час.Кроме того, опрос — чрезвычайно неэффективный процесс, только небольшая часть DOI когда-либо будет генерировать события, но нам придется опрашивать каждое из них, неоднократно, постоянно, чтобы получить точную картину активности DOI. Нам нужен был лучший способ. Нам нужно было посмотреть, можем ли мы обратить этот процесс вспять и убедить некоторые стороны вместо этого «проталкивать» нам информацию всякий раз, когда они видят события, связанные с DOI (например, цитирование, загрузки, публикации и т. Если бы только мы могли убедить кого-нибудь попробовать это…

Википедия События DOI

В декабре 2014 года мы воспользовались возможностью семинара PLOS / Crossref ALM 2014 в Сан-Франциско, чтобы встретиться с Максом Кляйном и Энтони Ди Франко, где мы начали очень захватывающий проект.

Всегда есть кто-то, редактирующий Википедию где-нибудь в мире. Фактически, вы можете увидеть головокружительный поток правок в прямом эфире. Мы подумали, что, учитывая, что в Википедии так много DOI, этот прямой эфир может содержать некоторые алмазы (DOI сделаны из алмаза, поэтому они могут быть постоянными). Макс и Энтони ушли и вернулись с демонстрацией, которая содержит удивительное количество активности DOI.

Эта демонстрация превращается в конкретный сервис под названием Cocytus. Он работает в Лаборатории Викимедиа, отслеживая изменения в реальном времени, пока вы это читаете.

На данный момент мы загружаем эти данные в приложение DOI Events Collection (которое является ответвлением проекта Chronograph). Мы находимся в процессе изменения кода Lagotto, чтобы вместо этого мы могли отправлять эти события в экземпляр отслеживания событий DOI.

Первое событие DOI, которое мы заметили, было восхитительно прозаичным: DOI для «Эрудитного проекта» цитируется на странице «Polymath Project» в Википедии. Возможно, это прозаично, но авторы этой статьи, вероятно, хотят знать. Может, они помогут отредактировать страницу.

Или как насчет этого. Кто-то написал статью о том, почему люди редактируют Википедию, а затем на нее процитировала Википедия. А потом цитата была удалена. Сюжет сгущается…

Нам интересно посмотреть, как DOI используются вне формальной научной литературы. Что это обозначает? Мы не совсем знаем, в этом вся суть. У нас есть опровержения в научной литературе (а наши метаданные и сервис Crossmark позволяют издателям записывать это), но в Википедии все немного по-другому. Править войны ведутся из-за … ну, вы сами в этом убедитесь.

Цитаты могут появляться и исчезать из статей. Мы видели, что DOI 10.1001 / archpediatrics.2011.832 был удален из «Биполярного расстройства у детей». Если бы мы не отслеживали прямую трансляцию (мы рассматривали возможность массового анализа снимков Википедии), мы, возможно, никогда бы этого не увидели. Это часть того, что означают нетрадиционные цитаты, и это не было очевидным, пока мы не увидели это.

Вы можете увидеть это действие в ленте Хронографа. Или проверьте свой любимый DOI. Имейте в виду, что на сегодняшний день мы собираем только недавно добавленные цитаты.Мы действительно намереваемся вернуться и заполнить заново, но это может занять некоторое время, так как * кашель * требует повторного опроса.

Некоторые технические детали

Несколько интересных вещей, которые произошли в результате всего этого:

Защищенные URL-адреса

SSL и HTTPS были изобретены, чтобы вы могли делать такие вещи, как банковские операции в Интернете, не опасаясь перехвата или вмешательства. Поскольку Интернет становится все более важной частью жизни, многие сайты переходят с HTTP на HTTPS, безопасную версию. Это связано не только с тем, что ваши конфиденциальные данные могут быть изменены, но и потому, что правительствам некоторых стран может не понравиться ваше чтение определенных материалов.

Из-за этого некоторое время назад Википедия решила приступить к обновлению до HTTPS в прошлом году, и они определенным образом продвигаются по этому пути. IDF, отвечающая за работу системы DOI, этим летом перешла на HTTPS, хотя большинство DOI по-прежнему используются по протоколу HTTP.

Мы встретились с Дарио Тараборелли на семинаре ALM и обсудили справочные данные DOI, которые вводятся в Хронограф. Мы соединили два и два и поняли, что Википедия ссылается на DOI (которые в основном являются HTTP) со страниц, которые могут обслуживаться через HTTPS.Новые политики в HTML5 определяют, что заголовки URL-адресов реферера не должны пересылаться с HTTPS на HTTP (если в них было что-то секретное). В результате, если кто-то просматривает Википедию через HTTPS и нажимает на обычный DOI, мы не узнаем, что пользователь пришел из Википедии. Сегодня это не большая проблема, но, поскольку Википедия переходит на полностью безопасный режим, мы упускаем очень полезную информацию.

К счастью, спецификация HTML5 включает способ исправить это (без утечки конфиденциальной информации). Мы обсудили это с Дарио, он провел небольшое исследование и выдвинул предложение, которое было обсуждено. Приятно наблюдать за подобным демократическим процессом и принимать в нем участие.

Мы ждем, чтобы увидеть, чем закончится обсуждение, и надеемся, что все это получится, и мы сможем продолжать сообщать о том, насколько великолепна Википедия в отправке людей за научной литературой.

Как мне процитировать тебя?

Из этого процесса выросла еще одна дискуссия, и мы начали разговаривать с википедистом по имени Немо (примечание для латинских ученых: мы не просто разговаривали сами с собой).У Немо (настоящее имя Федерико Лева) было несколько собственных предложений. Другой способ решить проблему реферера — использовать URL-адреса HTTPS (HTML5 позволяет браузерам отправлять домен реферера при переходе с HTTPS на HTTPS).

Это означает вернуться ко всем статьям, в которых используются DOI, и изменить их с HTTP на HTTPS. Не так просто, как кажется, и не кажется простым. Мы начали изучать, как DOI цитируются в Википедии.

После некоторых исследований мы обнаружили, что есть и другие способы цитирования DOI.

Во-первых, это URL. Вы можете увидеть это в действии в этой статье. URL-адреса могут принимать различные формы.

Во-вторых, официальный тег шаблона в действии:

  {{cite journal | title = Устойчивая миниатюризация и анатомические инновации динозавров-предков птиц | url = http: //www-sciencemag-org.turing.library.northwestern.edu/ content / 345/6196/562 | date = 1 августа 2014 | journal = [[Science (journal) | Science]] | volume = 345 | issue = 6196 | pages = 562–566 | doi = 10.1126 / science.1252243 | accessdate = 2 августа 2014 | last1 = Lee | first1 = Michael SY | first2 = Andrea | last2 = Cau | first3 = Darren | last3 = Naish | first4 = Gareth J. | last4 = Dyke}} 
 

Где-то там есть DOI. Это лучший способ цитировать DOI, во-первых, потому что на самом деле это правильное традиционное цитирование и в DOI нет ничего волшебного, во-вторых, потому что это тег шаблона, и при необходимости его можно изменить, чтобы он выглядел немного иначе.

В-третьих, старый официальный тег шаблона DOI, который сейчас не рекомендуется:

  {{Cite doi | 10. 1146 / annurev.earth.33.092203.122621}} 

И еще один.

 {{doi | 10.5555 / 123456789}}
 

Знание всего этого помогает нам находить DOI. Но если мы хотим преобразовать ссылки DOI в Википедии для использования HTTPS, это означает, что есть больше тегов шаблонов, которые нужно изменить, и больше страниц для повторного рендеринга.

Nemo также поместил DOI на карту Interwiki, что должно значительно упростить автоматическое изменение некоторых URL-адресов.

Мы очень благодарны Немо за его предложения и работу над этим.Мы ответим!

Слон в комнате

Те из вас, кто знает, как работают DOI, заметили в комнате незащищенного слона. Когда вы посещаете DOI, вы переходите по URL-адресу, который попадает на прокси-сервер преобразователя DOI, который возвращает в ваш браузер сообщение для перенаправления на целевую страницу на сайте издателя.

Безопасный обмен данными с преобразователем DOI с использованием HTTPS вместо HTTP означает, что никто не может подслушать и увидеть, какой DOI вы посещаете, или вмешаться в результат и отправить вас на другую страницу. Но страница, на которую вы отправляетесь, почти во всех случаях будет по-прежнему HTTP. Обновление инфраструктуры нетривиально, и с более чем 4000 участников (в основном издателей) большинство DOI Crossref в обозримом будущем по-прежнему будут перенаправлять на стандартные HTTP-страницы.

Вы можете обеспечить максимальную безопасность, используя HTTPS Everywhere.

Плавник

Здесь много всего происходит, смотрите это пространство, чтобы увидеть, что происходит. Спасибо, что прочитали это и все ссылки. Мы хотели бы знать, что вы думаете.

Bootnote

Вскоре после публикации этого сообщения в блоге мы увидели кое-что очень интересное.

Это не DOI.

Posted in Разное

Открытый чемпионат Великобритании (Эрудит) — frwiki.wiki

UK Open Эрудит является английский говоря Эрудит турнир под наблюдением Ассоциации игроков британского Эрудит .

Это самый важный англоязычный турнир по скрэбблу в Европе.

Год	Победитель	2- й	3- й	4 чт	5 чт	6 чт
2008 г.	Найджел Ричардс	Микки Николсон	Харшан Ламабадсурия	Марк Найман	Крейг Биверс	Джаред Робинсон
2009 г.	Хелен гипсон	Фил Робертшоу	Найджел Ричардс	Крейг Биверс	Микки Николсон	Харшан Ламабадсурия
2010 г.	Найджел Ричардс	Пол Аллан	Крейг Биверс	Крис мэй	Хелен гипсон	Микки Николсон
2011 г.	Найджел Ричардс	Натан Бенедикт	Алистер Ричардс	Стив полатник	Wale Fashina	Эд Мартин
2012 г.	Найджел Ричардс	Фил Робертшоу	Тох Вейбин	Крейг Биверс	Уэйн Келли	Мартин Харрисон
2013	Найджел Ричардс	Алистер Ричардс	Тереза ​​Бруссон	Крейг Биверс	Петр Андроновский	Стив полатник
2014 г.	Найджел Ричардс	Алистер Ричардс	Пол Аллан	Тереза ​​Бруссон	Тох Вейбин	Чжи Юань Вонг
2015 г.	Пол Аллан	Алистер Ричардс	Эли Дангур	Тереза ​​Бруссон	Азу Огбогу	Джессика праши
2016 г.	Найджел Ричардс	Кваку Сапонг	Уэйн Келли	Колин Нортмор	Ин Мин По	Джеймс Сквайрс
2017 г.	Найджел Ричардс	Остин Шин	Уэйн Келли	Винсент Бойл	Рафал Доминичак	Эли Дангур
2018 г.	Найджел Ричардс	Винсент Бойл	Джереми Ху	Чарльз Тачи-Менсон	Пол Аллан	Уэйн Келли
2019 г.	Найджел Ричардс	Остин Шин	Харшан Ламабадсурия	Рик Кеннеди	Ахмед Хан	Уэйн Келли

1. ↑ «  Рейтинговая статистика международных турниров, проведенных в 2008 г.  » , на members.ozemail.com.au (по состоянию на 27 февраля 2019 г. )
2. ↑ «  Рейтинговая статистика международных турниров, проведенных в 2009 г.  » , на members.ozemail.com.au (по состоянию на 27 февраля 2019 г. )
3. ↑ «  Рейтинговая статистика международных турниров, проведенных в 2010 г.  » , на members.ozemail.com.au (по состоянию на 27 февраля 2019 г. )
4. ↑ «  Положение 48 раунда Дивизиона A  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
5. ↑ «  Положение 38 раунда Дивизиона A  » на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
6. ↑ «  Положение 38 раунда UKopen 2013  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
7. ↑ «  Положение 30 раунда Дивизиона A  » , на сайте www.centrestar. co.uk (по состоянию на 27 февраля 2019 г. )
8. ↑ «  Положение 30 раунда A в дивизионе UKopen 2015  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
9. ↑ «  Положение 30 раунда A в дивизионе UKopen 2016  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
10. ↑ «  Положение за 30 тур UKopen 2017 Division A  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
11. ↑ «  Положение за 30 тур UKopen 2018 Division A  » , на сайте www.centrestar.co.uk (по состоянию на 27 февраля 2019 г. )
12. ↑ «  Положение за 30 тур UKopen 2019 Division A  » , на centrestar.co.uk (по состоянию на 27 февраля 2019 г. )

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

5 февраля поздравляем эрудитов

05. 02.2020 12:00

1859

Добавить в закладки

Эрудитом называют начитанного и образованного человека. И для того, чтобы считаться таковым, вовсе не обязательно иметь высшее образование. Достаточно любить книги и стремиться пополнить свой культурный и литературный «багаж». В то же время, образование также не тождественно эрудиции: обучение в вузе вовсе не всегда означает наличие статуса «эрудита» и книголюба. Широкий кругозор и обширные знания в различных сферах, как правило, это всегда результат собственных устремлений и самостоятельного развития. Чем обширнее прочитанная библиотека, тем больше вероятность называть такого человека эрудитом. И, конечно, есть особый праздник, посвященный данной категории людей — День эрудита. Пока он еще не вошел во всемирный календарь памятных дат, но неофициально его отмечают 5 февраля. Если вы любите читать, познавать мир и окружающую действительность, а книга – ваш неотъемлемый спутник и верный друг, то вас с полной уверенностью можно назвать эрудитом.  

Обратимся к происхождению слова. Латинское ēruditio означает учёность или просвещённость. То есть слово эрудиция определяет всестороннюю образованность и широкие познания в разных областях. В древние времена учёного считали эрудитом —  на латинском eruditus, если занятия и чтение, сопровождаемые осмыслением и выводами, вычеркнули всю его грубость — rudis, e-(ex-)+rudis, то есть «сгладили» его первоначальное невежество. 

Считается, что эрудиция характеризует образованного человека. Однако это не одно и то же. Человек-эрудит обязательно образован, но образованный человек — не обязательно эрудит. Различие в том, что человек-эрудит стремится преодолеть свою грубость и необразованность. Он вникает в конкретные темы непосредственно через книги и исследование, а не из курсов обучения предмету. В эпоху Просвещения эрудированность считалась частью идеи об идеальном человеке, который должен иметь знания учёного, навыки художника и тело атлета.

Среди известных эрудитов: Леонардо Да Винчи, Гёте, Бенджамин Франклин и, конечно, наш соотечественник Михаил Ломоносов. Эрудитом можете стать и вы, если придерживаться правильных жизненных установок. 

Чаще проявляйте любопытство. Эрудит — это не тот, кто стремится произвести впечатление или добиться славы. Ему просто хочется изучить всё, что касается интересных ему предметов. Никогда не поздно освоить доселе неизвестную область знаний. Тем более активное обучение улучшает работу мозга, а также помогает образованию новых нейронных связей, что снижает риск развития болезни Альцгеймера в старости.

Не ограничивайтесь лишь одним направлением. В отличие от узких специалистов, которые живут лишь своим предметом деятельности, эрудиты заинтересованы в изучении сразу нескольких областей знания. Исаак Ньютон и Рене Декарт были не только выдающимися математиками и физиками, но и философами, пытаясь разобраться в устройстве мира. 

Не будьте перфекционистом.  Все мы имеем ограниченное количество времени и энергии, поэтому не стоит стремиться быть экспертом во всех интересующих сферах. 

Ставьте перед собой выполнимые цели. Все известные истории эрудиты были неутомимыми и трудолюбивыми. И все они ставили реалистичные цели. Разбейте большие цели на малые, и каждый день оценивайте насколько вы были последовательны в своих стремлениях. И помните, успех каждого эрудита — это результат пронесённой через годы преданности науки и своему делу.

Автор Подготовила Анастасия Пензина

Образование эрудит эрудиция

Источник: kakoysegodnyaprazdnik.ru

Информация предоставлена Информационным агентством «Научная Россия». Свидетельство о регистрации СМИ: ИА № ФС77-62580, выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций 31 июля 2015 года.

НАУКА ДЕТЯМ

Академик Анатолий Деревянко объяснил, за что присудили Нобелевскую премию по медицине 2022

15:01 / Биология, История, Медицина

«Материя» в РХТУ на Фестивале НАУКА 0+

14:30 / Наука и общество, Химия

Нобелевскую премию по медицине 2022 присудили за изучение вымерших человекообразных обезьян и эволюции человека

14:15 / Биология, История, Медицина

Физики повысили эффективность адресной доставки лекарств с помощью мягких наногелей

13:30 / Медицина, Физика

Определен ген, отвечающий за формирование «скелета» клетки

13:15 / Биология

Научные бои психологов на Фестивале НАУКА 0+

12:30 / Наука и общество, Психология

Искусственный интеллект и количественная масс-спектрометрия предскажут исход заболевания COVID-19

11:30 / Медицина

«Первый женский университет». 144 года назад в Санкт-Петербурге открылись Высшие женские (Бестужевские) курсы

10:00 / История, Наука и общество, Образование

На волнах памяти. День рождения академика Константина Анохина

10:00 / Биология, Здравоохранение, Наука и общество, Персона

Ученые ЛЭТИ создали «Таблицу Менделеева» для систематизации элементов генетического кода

14:00 / Биология

Памяти великого ученого. Наука в глобальном мире. «Очевиднное — невероятное» эфир 10.05.2008

04.03.2019

Памяти великого ученого. Нанотехнологии. «Очевидное — невероятное» эфир 3.08.2002

04.03.2019

Вспоминая Сергея Петровича Капицу

14.02.2017

Смотреть все

Брифли — краткое содержание книг

• Недо­росль 🤪

  Денис Фонвизин · пьеса

  Злая жен­щина взяла в свой дом девушку-сироту. Дядя девушки решил оста­вить ей боль­шое наслед­ство, и жен­щина захо­тела выдать девушку замуж за сво­его глу­пого сына. Девушку спа­сли дядя и её воз­люб­лен­ный.

• Гра­на­то­вый брас­лет

  Куприн · рассказ

• Гроза

  Островский · пьеса

• Гос­по­дин из Сан-Фран­циско

  Бунин · рассказ

• Бед­ная Лиза

  Карамзин · повесть

• Олеся

  Куприн · повесть

• Житие Алек­сан­дра Нев­ского

  Древне­русская лит-ра · житие

• Фонвизин

  Не­до­росль · Бри­га­дир · Все­об­щая при­двор­ная грам­ма­ти­ка · Ко­ри­он, …

• Карамзин

  Бед­ная Лиза · На­та­лья, бо­яр­ская дочь · Остров Бор­н­гольм · Марфа-По­сад­ни­ца, …

• Пушкин

  Ка­пи­тан­ская дочка · Мед­ный всад­ник · Дуб­ров­ский · Ев­ге­ний Оне­гин · Цы­га­ны, …

• Гоголь

  Пе­тер­бург­ские по­ве­сти · Пор­трет · Нев­ский про­спект · Нос · Мёрт­вые души, …

• Тургенев

  Отцы и дети · За­пис­ки охот­ни­ка · Гам­лет Щи­гров­ско­го уезда · Муму · Ася · Щи, …

• Островский

  Гроза · Бес­при­дан­ни­ца · Свои люди — со­чтём­ся · Сне­гу­роч­ка · Лес · Ди­кар­ка, …

• Чехов

  Виш­нё­вый сад · Ма­лень­кая три­ло­гия · Ионыч · Кры­жов­ник · Че­ло­век в фу­тля­ре, …

• Горький

  На дне · Ста­ру­ха Изер­гиль · Макар Чудра · Чел­каш · Данко · Васса Же­лез­но­ва, …

• Бунин

  Тём­ные аллеи · Гос­по­дин из Сан-Фран­цис­ко · Чи­стый по­не­дель­ник · Де­рев­ня, …

• Куприн

  Гра­на­то­вый брас­лет · Олеся · По­еди­нок · Чу­дес­ный док­тор · Су­ла­мифь · Яма, …

• Как завоё­вы­вать дру­зей

  Дейл Карнеги · бизнес

  Улы­байтесь, помните имя собе­сед­ника, про­яв­ляйте инте­рес к его темам, слу­шайте, искренне хва­лите, не кри­ти­куйте и не спорьте. Если неправы — сразу при­знайте. Убе­ждайте в своей пози­ции мето­дом Сократа.

• Пси­хо­ло­гия вли­я­ния

  Чалдини · психология

• Госу­дарь

  Макиавелли · философия

• О ско­ро­теч­но­сти жизни

  Сенека · философия

• Кради как худож­ник

  Клеон · искусство

• Хочу и буду

  Лабковский · психология

• Искус­ство войны

  Сунь-цзы · философия

• Пре­ступ­ле­ние и нака­за­ние 🪓

  Фёдор Достоевский · роман

  Нищий сту­дент убил ста­руху-про­цент­щицу, но исполь­зо­вать её богат­ство на благо ближ­них не успел. Из-за мук сове­сти и нерв­ной лихо­радки он при­знался в соде­ян­ном и после суда отпра­вился на каторгу.

• Малень­кий принц 🌹

  А. де Сент-Экзюпери · повесть

  Лёт­чик встре­тил маль­чика, путе­ше­ству­ю­щего среди звёзд, и они подру­жи­лись. Маль­чик рас­ска­зал лёт­чику о своём путе­ше­ствии и о род­ной пла­нете, а потом вер­нулся домой, где его ждала люби­мая роза.

• При­клю­че­ния капи­тана Врун­геля

  Андрей Некрасов · повесть

  Капи­тан с мат­ро­сами отпра­вился в кру­го­свет­ное пла­ва­ние. Они посе­тили много стран, пере­жили и при­клю­че­ния, и неудачи: их пре­сле­до­вали, команда раз­де­ля­лась, яхта лома­лась, но они завер­шили путе­ше­ствие.

• Вождь крас­но­ко­жих

  О. Генри · рассказ

  Сына бога­того фер­мера похи­тили и потре­бо­вали выкуп. Маль­чишка-хули­ган довёл своих похи­ти­те­лей до нерв­ного срыва. Они вер­нули его отцу, но тот не хотел заби­рать сво­его хули­гана, пока ему не запла­тили.

• Фрёкен Жюли

  Август Стриндберг · пьеса

  Дочь графа отда­лась лакею. Она украла деньги отца, чтобы сбе­жать с любов­ни­ком, и пред­ло­жила ему уме­реть вме­сте, если их союз будет несчаст­ным. Но он отка­зался и при­ка­зал ей пере­ре­зать себе горло.

• Мак­симка 👦🏾

  К. М. Станюкович · рассказ

  Корабль подо­брал в море чер­но­ко­жего маль­чика. Команда полю­била его, а один из мат­ро­сов взялся за вос­пи­та­ние. Ребёнка окре­стили и при­няли в мат­росы. Он выучил рус­ский язык и стал учиться на фельд­шера.

• Лёг­кое дыха­ние

  Иван Бунин · рассказ

  Вет­ре­ную гим­на­зистку лишил невин­но­сти взрос­лый муж­чина. Затем она увле­клась про­стым офи­це­ром. Тот хотел жениться на ней, но девушка при­зна­лась, что моро­чила ему голову. Обма­ну­тый офи­цер застре­лил её.

• Ворон-чело­бит­чик

  Салтыков-Щедрин · сказка

  Ста­рый ворон, спа­сая свой род, истреб­ля­е­мый людьми и хищ­ни­ками, начал искать правды у началь­ства и дошёл до кор­шуна. Тот объ­яс­нил, что время его правды ещё не при­шло, но в буду­щем она всех объеди­нит.

• При­клю­че­ние с Кра­моль­ни­ко­вым

  Салтыков-Щедрин · сказка

  Писа­тель понял, что его нет. Чита­тели отвер­ну­лись от него. Выяс­ни­лось, что твор­че­ство было бес­плод­ным, так как он не затра­ги­вал про­блемы про­ти­во­­сто­я­ния есте­ствен­ных побу­жде­ний и духов­ных цен­но­стей.

• Дере­вен­ский пожар

  Салтыков-Щедрин · сказка

  Деревня сго­рела, а вме­сте с ней сын одной из житель­ниц. Добрая барыня пожерт­во­вала ей денег, но несчаст­ная мать отка­за­лась. Потом деревня отстро­и­лась заново, но мать погиб­шего ребёнка исчезла.

• Кисель

  Салтыков-Щедрин · сказка

  Кухарка сва­рила для гос­под кисель. Сна­чала он всем нра­вился, но потом гос­пода отка­за­лись от киселя и уехали. Кисель съела сви­нья. Всё про­гу­ляв, гос­пода вер­ну­лись и уви­дели, что кисель закон­чился.

• Баран-непо­мня­щий

  Салтыков-Щедрин · сказка

  Баран уви­дел сон, но не смог его вспо­мнить. Он стал тре­вож­ным и пере­стал обра­щать вни­ма­ние на овец. Его высекли, но не помо­гло — баран начал видеть сны посто­янно. Он ото­щал, поте­рял силы и умер.

ГЛАВНАЯ | Polymath REU

Совместные математические исследования студентов бакалавриата

Polymath Jr.

Новости:

• Поздравляем нашу группу «Различные расстояния 2020» с получением награды «Молодые исследователи»! Эта премия в размере 1000 долларов предназначена для публикаций авторов моложе 35 лет, в то время как им было меньше 25 лет!

• Приветствуем новый Вьетнамский полимат REU! Мы рады найти способы сотрудничества с вами.

  

​

 

Программа

Наша цель – предоставить исследовательские возможности каждому студенту, желающему изучать высшую математику. Программа состоит из исследовательских проектов по различным математическим темам и проходит в духе проекта Polymath. Каждый проект курируется активным исследователем с опытом наставничества студентов.

​

Каждый проект состоит из 20-30 студентов, основного наставника и дополнительных наставников (обычно аспирантов). Эта группа работает над решением исследовательской проблемы и написанием статьи. Каждый участник решает, что он хочет получить от программы, и соответственно участвует.

 

Программа частично поддерживается премией NSF DMS-2218374.

 

(Полная информация представлена ​​ниже.)
 

2022 Наставники и проекты (Все еще обновляется)

Рикардо Баптиста (MIT) работает над масштабируемыми алгоритмами для вероятностного моделирования и байесовского вывода.

​

На Polymath Jr 2022 Рикардо будет руководить проектом по машинному обучению. Появится больше информации.

 

Жанар Бериккызы (Университет Фэрфилда) занимается комбинаторикой, теорией графов и приложениями. Она является соорганизатором программы летних математических исследований в Университете Фэрфилда.

​

На Polymath Jr 2022 Жанар будет руководить проектом TBD

Анураг Бишной (Технический университет Делфта, Нидерланды) занимается экстремальной комбинаторикой, конечной геометрией и алгебраической теорией графов.

​

На Polymath Jr 2022 года Анураг будет одним из руководителей специального проекта по теории Рэмси. Дополнительную информацию см. здесь.

Бен Брубейкер (Университет Миннесоты) занимается аналитической теорией чисел и теорией представлений. Был наставником в программе УМН РЭУ, а также координатором программы.

​

На Polymath Jr 2022 Бен будет вести проект по решетчатым моделям. Нажмите сюда, для получения дополнительной информации.

Марион Кампизи (Государственный университет Сан-Хосе) занимается геометрической топологией, трехмерными многообразиями, теорией узлов и мошенничеством.

​

На Polymath Jr 2022 Марион будет руководить проектом по комбинаторной теории узлов. Дальнейшие подробности появятся в ближайшее время.

Джоанна Франклин (Университет Хофстра) занимается теорией вычислимости и ее приложениями к вероятности и анализу.

​

На Polymath Jr 2022 Франклин будет вести проект по математической логике. Нажмите сюда, для получения дополнительной информации.

Луис Дэвид Гарсия Пуэнте (Колледж Колорадо) занимается алгебраической статистикой, алгебраической комбинаторикой, прикладной и вычислительной алгебраической геометрией, а также комбинаторной коммутативной алгеброй. Более 20 лет он курирует исследовательские проекты студентов, в том числе в качестве научного наставника MSRI-UP 2016 года.

​

На Polymath Jr 2022 Луис будет одним из руководителей специального проекта по теории Рэмси. Дополнительную информацию см. здесь.

Анантнараян Харихаран (IIT Bombay) занимается коммутативной алгеброй и гомологической алгеброй.

​

На Polymath Jr 2022 Анант будет вести проект по коммутативной алгебре. Более подробная информация появится.

Стивен Миллер (Колледж Уильямс) занимается аналитической теорией чисел, теорией случайных матриц и вероятностью. Он был директором программы МАЛЫЙ РЭУ более десяти лет.

​

На Polymath Jr 2022 Стивен будет вести проект по теории чисел. Дополнительную информацию см. здесь.

Виктор Молл (Университет Тулейна) занимается специальными функциями, теорией чисел и символьными вычислениями. Более 20 лет он руководил исследовательскими проектами студентов.

​

На Polymath Jr 2022 Виктор будет вести проект по интегральной оценке. Появится больше информации.

Наташа Моррисон (Университет Виктории, Канада) занимается экстремальной, вероятностной и аддитивной комбинаторикой.

​

На Polymath Jr 2022 Наташа будет одним из руководителей специального проекта по теории Рэмси. Дополнительную информацию см. здесь.

Джулио Трихила (CUNY) работает в области оптимизации, машинного обучения, прикладной теории вероятностей и вычислительной физики.

​

На Polymath Jr 2022 Джулио будет руководить проектом по машинному обучению. Появится больше информации.

Адам Шеффер (CUNY) работает в области комбинаторной геометрии и аддитивной комбинаторики. Он руководит NYC Discrete Math REU.

 

На Polymath Jr 2022 Адам станет одним из руководителей специального проекта по теории Рэмси. Для получения дополнительной информации см. здесь.

Коди Стокдейл (Университет Клемсона) занимается анализом, особенно гармоническим анализом, теорией операторов и комплексными переменными.

​

На Polymath Jr 2022 Коди будет руководить проектом по гармоническому анализу. Дополнительную информацию см. здесь.

Юнус Зейтунку (Мичиганский университет в Дирборне) занимается комплексным анализом. Он руководит REU UM-Dearborn по математическому анализу.

​

На Polymath Jr 2022 Юнус запустит проект эллипсы, числовой диапазон, пространства Харди и теорему Понселе. Дальнейшие подробности появятся в ближайшее время.

Алекс Зупан (Университет Небраски-Линкольн) занимается геометрической топологией, низкоразмерной топологией и теорией узлов.

​

На Polymath Jr 2022 Алекс будет руководить проектом по презентациям симметричного объединения для ленточных ссылок. Нажмите сюда, для получения дополнительной информации.

Участие в программе, но не наставничество в 2022 г.

Кира Адаричева (Университет Хофстра) занимается универсальной алгеброй, теорией решеток и выпуклой геометрией. Ее наставничество в области исследований для студентов привело к публикации статей по различным темам.

Соён Ким (Королевский университет). Ким руководил исследовательскими проектами бакалавриата в Университете Брауна и в SMALL REU Колледжа Уильямс. Она также участвует в программе наставничества Girls sySTEM для старшеклассников в Онтарио, Канада.

Пэт Девлин (Йельский университет) занимается вероятностной и экстремальной комбинаторикой. Он был наставником и координатором Йельской программы SUMRY REU.

Александра Сечелану (Университет Небраски-Линкольн) занимается коммутативной алгеброй с геометрическим и вычислительным уклоном.

​

Кристофер О’Нил (Государственный университет Сан-Диего) О’Нил работает на стыке коммутативной алгебры
, дискретной оптимизации и теории полугрупп, используя методы алгебраической
и перечислительной комбинаторики. Является научным руководителем СДСУ РЭУ.

Эрик Роуленд (Университет Хофстра) изучает арифметические свойства целочисленных последовательностей, возникающих в комбинаторных условиях.

​

​

Энрике Тревиньо (колледж Лейк-Форест) занимается аналитической и вычислительной теорией чисел. Он главный редактор USAMO.

 

Многие другие подробности

Цель оригинального проекта Polymath — решать проблемы путем организации онлайн-сотрудничества между многими математиками. Это делается через специальный вики-сайт. Это включает в себя давние открытые проблемы и некоторых ведущих математиков мира.

​

Программа Polymath Jr – это студенческая версия проекта Polymath. Он фокусируется на более скромных открытых проблемах, обычно таких, которые не требуют значительной подготовки. Однако эти проблемы по-прежнему представляют интерес для научного сообщества, и результаты должны быть опубликованы в научном журнале.

​

Исследовательские проекты.​

• Программа продлится с 20 июня по 14 августа.

• Это онлайн-программа. В рабочих целях мы полагаемся на выделенный вики-сервер, серверы Discord, обратную сторону, Zoom и многое другое.

• Первая неделя посвящена изучению различных проектов. К концу этой недели вы ранжируете интересующие вас проекты.

• Последние выходные — онлайн-конференция, на которой каждая группа представляет свою работу.

• Помимо основного наставника, в каждый проект входят дополнительные наставники. Обычно это аспиранты, а также постдоки и опытные студенты.

• Мы призываем участников к как можно большему взаимодействию. Это включает в себя регулярные рабочие встречи, а также социальные встречи (например, для игр).

• Все участники проекта, которые были активны на протяжении всей программы, имеют свои имена на бумаге (иногда под псевдонимом Поли Мэтьюз-младший, с настоящими именами в сноске). Это может показаться несправедливым по отношению к ученикам, добившимся значительного прогресса. Тем не менее, эти студенты могут получить сильное рекомендательное письмо от главного наставника. Такое письмо обычно гораздо важнее при поступлении в аспирантуру или на работу, связанную с исследованиями.

• Вы выбираете уровень участия. Совершенно нормально участвовать в программе неполный рабочий день. Многие участники могут не совершить научного прорыва, и это нормально. Вы можете внести свой вклад, помогая с веб-сайтом, помогая писать, организовывая общественные мероприятия и многое другое. Вы также можете принять незначительное участие, просто чтобы получить первое впечатление о том, как выглядит исследование.

• Цитаты из недавних опросов по окончании программы:​​

  • «Мне больше всего нравилось читать литературу и собирать данные, которые подтверждали бы или опровергали наши предположения».

  • «Мне больше всего понравились люди в программе.»

  • «Я действительно наслаждался свободой исследовать то, что меня больше всего интересовало в рамках моего проекта.»

  • «Мне больше всего нравилось придумывать сумасшедшие концепции и обсуждать их, чтобы люди не отмахивались от тебя сразу.»

  • «Это был мой первый исследовательский опыт, поэтому было очень приятно увидеть, как проводятся исследования, и внести в них некоторые результаты.»

  • «Хоть я и не вношу большого вклада в группу, я с удовольствием учился тому, что мог, и ставил перед собой задачи, выполняя упражнения. »

  • «Моей любимой частью была презентация.»

  • «Моей любимой частью программы было то, что люди, увлеченные математикой, могли поговорить с ними о математике».​

​

Подача заявки на участие в программе.

• Принятие не происходит автоматически. Тем не менее, программа открыта для большинства студентов, имеющих опыт написания математических доказательств.

• Ограничений по гражданству нет, и участники могут находиться в любой точке мира. Тем не менее, онлайн-встречи, скорее всего, будут проводиться в соответствии с графиком работы в США.

• Участие бесплатное, но финансирование для участников не предусмотрено.

• Участники должны быть студентами бакалавриата. Студенты, которые поступают в колледж следующей осенью или заканчивают колледж этой весной, имеют право подать заявку, но им будет отдан более низкий приоритет.

  • Студентов, обучающихся перед первым семестром в колледже, просят подробно объяснить, как они уже имеют опыт написания математических доказательств.

  • Студенты, только что окончившие колледж, получат более высокий приоритет, если у них нет предыдущего исследовательского опыта (или они попали в необычные обстоятельства).

• Если вы участвуете в программе в стиле REU летом 2022 года, мы настоятельно рекомендуем не присоединяться к этой. Участие в двух программах, скорее всего, приведет к плохим результатам в обеих. Если вы настаиваете, предоставьте письмо от другой программы о том, что они это одобряют.

​

​

Мы больше не принимаем заявки на участие в программе 2022 года.

• Заявки подаются через mathprograms.org.

• В математических программах в полях «год» и «месяц» обязательно укажите предполагаемую дату (или прошедшую дату), когда вы закончите (d) получение степени бакалавра.

• Укажите учебное заведение, в котором вы получили степень бакалавра.

• В вашем заявлении должно быть указано, что вы прошли курс математических доказательств. Другие официальные программы, обучающие написанию корректуры, также действительны. (Например, математический кружок.)

• Сопроводительное письмо может быть очень коротким. Это нормально, если он включает только ваш опыт написания корректуры. Если вы хотите, вы можете указать любую дополнительную информацию: особые обстоятельства, почему вы хотите участвовать в программе, ваш опыт или что-то еще.

• Требуется рекомендательное письмо хотя бы от одного профессора математики.

• Вы можете включить любую дополнительную информацию, такую ​​как резюме, дополнительные письма и предыдущие исследования. Однако это не обязательно для входа в программу.

• Нет необходимости указывать, какой проект вас интересует. 

​

Для получения дополнительной информации см. эту статью, опубликованную в Извещениях Американского математического общества.

​

С любыми дополнительными вопросами или комментариями обращайтесь к Адаму Шефферу по адресу adam. [email protected].

​

​

Логотип Polymath Jr был создан Луизой Эстрада. Дополнительный логотип создан Huiwen Lu.

​

​

Список эрудитов — EveryoneWiki Bios & Wiki

From EveryoneWiki Bios & Wiki

Перейти к:навигация, поиск

Эта статья посвящена конкретным примерам эрудитов. Страница является подмножеством родительской статьи Polymath. Чтобы узнать о других значениях, см. Список эрудитов (значения).

Эрудит (греч. πολυμαθής, polymathēs , «многому научившись», ^[1] латынь: homo universalis, «универсальный человек» ^{[2] 903 значительное количество различных предметных областей — такой человек, как известно, использует сложные своды знаний для решения конкретных проблем.}

Содержание

• 1 Предлагаемые критерии
• 2 Список эрудитов
• 3 См. также
• 4 Дополнительная литература
• 5 Каталожные номера

Предлагаемые критерии[править]

Критерии того, кого можно считать эрудитом мирового уровня, должны быть строго определены и соответствовать высоким стандартам, чтобы этот список не был слишком длинным. Этот человек должен иметь заметные достижения в нескольких РАЗНЫХ и НЕСВЯЗАННЫХ предметных областях, как правило, как в искусстве, так и в науке. Например, достижения в биологии, химии и физике считаются родственными, поскольку все три относятся к области естествознания.

Не связанные предметные области в этом списке, идентифицированные 13 подкатегориями, такими как изобразительное искусство, естественные науки, инженерия. Подкатегория «Другое» может включать дополнительные виды деятельности, такие как вычислительная техника, сельское хозяйство или спорт.

1. Что касается этого списка, эрудит, указанный здесь, должен иметь заметные достижения по крайней мере в пяти из тринадцати подкатегорий, включая как минимум одну подкатегорию искусств.
2. Значимость достижения определяется фактом его наличия в соответствующей статье Википедии. Примеры достижения: рукопись, художественная выставка, музыкальная пластинка, печатное издание, фильм, изобретение, научное открытие, крупная награда, вклад в преподавание, руководство бизнесом/военными/государством.

Список эрудитов[править]

Этот список неполный; Вы можете помочь, расширив это.

Список данных на основе соответствующих статей Википедии

Имя	Родился	Национальность	Искусство				Фундаментальные науки			Прикладные науки
			Изобразительное искусство	Литературное искусство	Исполнительское искусство и кино	Прикладное искусство	Формальные науки	Естествознание	Общественные науки	Архитектура	Образование	Машиностроение	Здоровье	Менеджмент	Другое
Аристотель	-384	Македонская империя (греческая)		Теория искусств и критика			Логика	Физика, астрономия, биология, геология, психология	Этика, философия, экономика, политика		Учитель философии	Классическая механика, Оптика		Теория государственного управления
Мунтадер Салех	1999 г.	Республика Ирак (Иракская)	3D-слои, иллюстрации, книжная скульптура, линии, каллиграфия	Цитаты	Дизайнер	Теория искусства		Фармацевт
Птолемей	100	Египет, Римская империя (греч.)		Поэзия	Теория музыки		Математика	Астрономия, астрология, география	Философия			Оптика
Авиценна	980	Империя Саманидов Зиярид Табаристан Буид Персия (персидский)		Поэзия			Логика	Физика, химия, астрономия, астрология	Философия		Учитель		Медицинская энциклопедия
Леонардо да Винчи	1452	Флорентийская Республика (итал. )	Картины, рисунки, фрески, скульптура	Поэзия	Музыка (Лира)		Математика	Физика, анатомия, физиология	Теория искусства	Архитектура, Градостроительство, Мосты	Учитель рисования	Вертолет, Летательная машина, Подводная лодка, Оптика, Гидродинамика, Музыкальные инструменты, Механический рыцарь, Гидравлические насосы, Кривошипные реверсивные механизмы, Оребренные минометные снаряды, Парашют, Паровая пушка, Самоходная машина	Кулинария
Готфрид Вильгельм Лейбниц	1646	Электорат Саксонии, Священная Римская империя (немецкий)		Поэзия		Теория игр	Математика, логика	Физика, космология, эмбриология, палеонтология	Филология, философия, правоведение, китаеведение, экономика, психология		Программа медицинской подготовки	Механика, Ветряные двигатели, Водяные насосы, Горнодобывающие машины, Гидравлические прессы, Лампы, Подводная лодка, Часы, Паровой двигатель	Медицинское письмо	Дипломатия
Михаил Ломоносов	1711	Царство Российское (рус. )	Мозаика	Поэзия				Физика, география, химия, геология	История, филология		Профессор	Телескоп-рефлектор

См. также[править]

• Искусство
• Очерк науки
• Очерк прикладной науки
• Компетентный человек
• Гений
• Мастер на все руки, мастер ни в чем
• Многофункциональность
• Опсимат
• Филомат
• Полиглотизм

Дополнительная литература[править]

• Введение в гуманитарные науки. Список полиматов
• Величайшие эрудиты в истории и советы, которые они оставили после себя

Ссылки[править]

1. ↑ Термин был впервые записан в письменном английском языке в начале семнадцатого века Harper, Daniel (2001). «Онлайн- этимологический словарь» . Проверено 5 декабря 2006 г.
2. ↑ «Спросите философа: Тим Саутфоммасан — В поисках человека эпохи Возрождения». Австралиец. 10 апреля 2010 г. Проверено 27 июля 2018 г.

Эта статья «Список эрудитов» взята из Википедии. Список его авторов можно увидеть в его истории и/или на странице Edithistory:List of polymaths. Статьи, скопированные из чернового пространства имен в Википедии, можно было увидеть в черновом пространстве имен Википедии, а не в основном. 907:30

определение эрудита в The Free Dictionary

Также найдено в: Thesaurus, Medical, Wikipedia.

полиматематика

 (pŏlē-măth’)

сущ.

Человек с большим или разносторонним образованием.

---

[греч. polumathēs: полу-, поли- + мантанеин, математика-, учиться ; см. mendh- в индоевропейских корнях.]

---

поли·математика , поли·математика прил.

po·lym’a·thy (pə-lĭm’ə-thē) н.

Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

эрудит

(ˈpɒlɪˌmæθ)

n

человек с большими и разнообразными знаниями

[C17: от греческого polumathēs обладающий большими знаниями]

3

ˌpolyˈmathic adj

polymathy n

Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014

pol•y•math

(ˈpɒl iˌmæθ)

сущ.

человек с большими знаниями в нескольких областях знаний; полиистор.

[1615–25; <греческий эрудит ученый = поли- поли- + -mathēs, прил. производное от мантанеин учиться]

полиматематика, прил.

po•lym•a•thy (pəˈlɪm ə θi) н.

Рэндом Хаус Словарь колледжа Кернермана Вебстера, © 2010 K Dictionaries Ltd. Авторские права Random House, Inc., 2005, 1997, 1991. Все права защищены.

ТезаурусАнонимыРодственные словаСинонимы Легенда:

Перейти к новому тезаурусу

Существительное

1.

Polymath — человек великого и разнообразного обучения Ученый человек, Pundit, Savant.

На основе WordNet 3.0, коллекции клипартов Farlex. © 2003-2012 Принстонский университет, Farlex Inc.0003

Polymathe

Persona Con Cultura Enciclopedica

Polymath

[ˈpɒlɪmæθ] N → Polímata MF , Erudito/A M/F

910.IMILINSIRINMIRINMIRININGINMIRINMIRINIARIRIINTIRINITIRINIARIRINIARIRINIARIRINIARIRINIARIRINIARIRIINTION

. & Co. Ltd., 1971, 1988 © HarperCollins Publishers, 1992, 1993, 1996, 1997, 2000, 2003, 2005

Немецкий словарь Коллинза – полное и полное, 7-е издание, 2005 г. 80 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007

Упоминается в ?

• Alhacen
• Al-Hasan ibn al-Haytham
• al-Haytham
• Alhazen
• Ibn al-Haytham
• initiate
• knowledge
• learned person
• polyhistor
• polymathy
• pundit
• savant

Ссылки в архиве периодических изданий ?

ГОНКОНГ, 17 июня 2019 г. — (ACN Newswire) — Ведущая платформа токенов безопасности Polymath сегодня объявила о стратегическом сотрудничестве с решением для проверки цифровой идентификации Blockpass.

Polymath и Blockpass объявляют о стратегическом сотрудничестве и партнерстве

BTCNYEX в настоящее время предлагает живое предложение STO — токен ST20 (BNYX), созданный в сотрудничестве с Polymath. Токен BNYX ST-20 является расширением токена Ethereum ERC-20 и предоставляет возможность ограничивать передачу токенов блокчейна.

Крипто А.М. освещает BTCNYEX.COM

Резюме: Матхурапур (Западная Бенгалия) [Индия], 16 мая (ANI): Через несколько часов после того, как Нарендра Моди пообещал установить грандиозную статую Ишвара Чандры Видьясагара на том же месте, где стояла старая статуя до того, как подверглась вандализму , Мамата Банерджи парировала и утверждала, что у Западной Бенгалии есть деньги, необходимые для структуры эрудита, и спросила, может ли премьер-министр вернуть 200-летнее наследие.

У Бенгалии есть деньги, чтобы сделать статую Видьясагара: Мамата наносит ответный удар Моди

Несколько лет назад Эдвард де Боно (Эрудит, изобретатель «латерального мышления») решил разработать простую игру, дающую равные шансы обоим игрокам, и создал L-игру.

Одна буква «L» в игре: Colin Ledsome CEng FIED представляет увлекательную простую игру для двух человек. Спойлер: это может вызвать привыкание!

Другое значение слова «хаким» означает человека с большими знаниями, философа или эрудита.

Литературные заметки: аутентичный труд по истории и народной медицине

БАНКОВСКИЕ И КРЕДИТНЫЕ НОВОСТИ — 9 января 2019 г. — LeadBest, партнер Polymath по созданию экосистемы экономики токенов

LeadBest, партнер Polymath по созданию экосистемы экономики токенов экосистема

LeadBest, партнер Polymath по созданию экосистемы экономики токенов

Global Banking News — 9 января 2019 г. — LeadBest, партнер Polymath по созданию экосистемы экономики токенов

LeadBest, партнер Polymath по созданию экосистемы экономики токенов

627-1229), сирийский эрудит и епископ Иаков из Эдессы, политическая система джамахирии Муаммара Каддафи (1942-2011) в Ливии и старая мусульманская община в индийском городе Кожикоде.

The Encyclopaedia of Islamic — Three 2019-1

В нем есть подходящий актерский состав, в центре которого герой, гарвардский профессор Роберт Лэнгдон, героиня и гений-энциклопедист, который построил компьютер по имени Уинстон, который может делать практически все.

Происхождение: Роман

Один экземпляр также был подарен королеве Елизавете II. 7 ноября в Британской библиотеке в Лондоне состоялась реклама самого первого перевода «Кровавых сонетов», написанного словацким поэтом и эрудитом Паволом Оршакутехом Гвездославом.

Первый английский перевод «Кровавых сонетов» представлен в Лондоне

Высшим примером ценности междисциплинарных исследований является эрудит: мужчина или женщина эпохи Возрождения.

Междисциплинарные исследования

Браузер словарей ?

• ▲
• polyhedron
• polyhedrosis
• Polyhedrous
• polyhidrosis
• polyhistor
• polyhistoric
• polyhistory
• polyhybrid
• polyhydramnios
• polyhydric
• polyhydroxy
• Polyhymnia
• polyimide
• Polyiodide
• polyisoprene
• полилемма
• полилингва
• полилогия
• Polyloquent
• polylysine
• polymastia
• polymastic
• Polymastigina
• polymastigote
• polymastism
• polymath
• polymathic
• Polymathist
• polymathy
• Polymeniscous
• polymer
• polymerase
• polymerase chain reaction
• polymeric
• полимерамид
• полимеризация
• полимеризация
• полимеризация
• polymerization
• polymerize
• polymerous
• polymery
• polymetallism
• polymethyl methacrylate
• Polymnia
• Polymnite
• Polymonium caeruleum van-bruntiae
• polymorph
• polymorphemic
• polymorphic
• polymorphic function
• ▼

Полный браузер ?

перевод на китайский язык: Cambridge Dict.

(Перевод polymath из Cambridge English-Chinese (Simplified) Dictionary © Cambridge University Press)

Примеры полимата

полимата

Он был настоящим эрудитом , написал ряд стихов, опубликовал несколько романов и сочинил песни.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Он был эрудитом и проводил исследования в области геологии, минералогии, ботаники, химии, этнографии, петрологии и карстологии.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Мы думали, что он исчерпал все свои силы и ничего не знал о его эрудированном характере.

Из Кембриджского корпуса английского языка

Читатели закончат книгу вполне удовлетворенными и, если только они не настоящие исторические эрудиты, будут гораздо лучше информированы, чем были до того, как начали читать.

Из Кембриджского корпуса английского языка

Такую работу не мог бы написать или рецензировать один человек, так как необходимой эрудиции сегодня нет даже у одного человека.1096 эрудит .

Из Кембриджского корпуса английского языка

Что-то вроде эрудита , он установил связи между дисциплинами и отстаивал идею о том, что фотосинтез был принят бактериями, которые возникли с морского дна и впоследствии колонизировали сушу.

Из Кембриджского корпуса английского языка

Я отдаю ему должное за то, что он инициировал дискуссию и предоставил нам всю информацию, а также за то, что он был настоящим эрудитом — инженером, который может исправлять собственные герундии.

С

Архив Hansard

Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0

.

Чтобы освещать поднятые темы, нужно быть кем-то вроде эрудита .

С

Архив Hansard

Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0

.

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.

Переводы слова polymath

на китайском (традиционный)

博學的人…

Подробнее

на португальском

polimata…

Подробнее

Нужен переводчик?

Получите быстрый бесплатный перевод!

Посмотреть определение polymath в словаре английский языка

Обзор

многоугольник

полиграф

многоженство

многогранник

полимат

полимер

полимеризация

полимеризоваться

полиморфизм

Возможные будущие проекты Polymath (2009, 2021)

Каким будет наш следующий проект Polymath?

Проект эрудита (Википедия) — это совместная работа математиков для решения важных и сложных математических задач путем координации многих математиков для общения друг с другом в поиске наилучшего пути к решению. Проект стартовал в январе 2009 года.в блоге Тимоти Гауэрса, когда он опубликовал проблему и попросил своих читателей публиковать частичные идеи и частичное продвижение к решению. Этот эксперимент привел к новому ответу на сложную проблему, и с тех пор проект Polymath расширился до описания конкретного процесса использования онлайн-сотрудничества для решения любой математической задачи.

После успеха Polymath2 и запуска Polymath4 и Polymath5 Тим Гауэрс написал в своем блоге сообщение «Возможные будущие проекты Polymath» для планирования следующего проекта Polymath. В сообщении упоминается 9возможные проекты. (Трое из них впоследствии обратились к эрудитным проектам, а один превратился в проект иного характера.) Вслед за постом и отдельными постами с описанием некоторых из предложенных проектов было проведено несколько опросов, и была поставлена ​​проблема – проблема несоответствия Эрдёша. выбран для следующего проекта polymath5.

Один из наших следующих постов будет иметь то же название и ту же цель, что и пост Тима 2009 года. Я опишу несколько возможностей для моего следующего полиматического проекта. (Быстрый, довольно расплывчатый и предварительный предварительный просмотр можно найти в конце этого поста. ) Сегодня мы вернемся к посту Тима от 2009 года и проблемам, изложенным в нем.

Приветствуются комментарии по предлагаемым проектам 2009 года, новым предлагаемым проектам, другим предлагаемым проектам, а также по эрудитным усилиям. (В конце поста я также упоминаю несколько «мета-вопросов».)

Позвольте мне также упомянуть проект PolyTCS, направленный на предложение проектов в области теоретической информатики. На данный момент есть три очень интересных предложения, и первое предложение — это гипотеза Фридгута-Калаи об энтропии/влиянии. Различные предложения см. также в блоге эрудитов, который ведут Тим ​​Гауэрс, Майкл Нильсен, Терри Тао и я, и в этом вопросе МО.

Предлагаемые проекты в сообщении Гауэрса от 2009 года и обновления, касающиеся этих проектов.

1. Гипотеза Литтлвуда и связанные с ней проблемы.

Гипотеза утверждает, что если  и  являются любыми двумя действительными числами, и , то существует натуральное  такое, что . Известно, что Эйнзидлер, Каток и Линденштраус доказали, что размерность Хаусдорфа множества контрпримеров к гипотезе равна нулю. У Гауэрса были идеи для элементарного подхода, и его идеи описаны в этом посте. Этот проект не был запущен, и я также не в курсе прогресса, связанного с проблемой (но я не эксперт).

2. Проект, связанный с DHJ.

DHJ расшифровывается как «плотность Хейлза Джуэтта», которая была темой эрудиты2. Второй предложенный проект должен был развить успех polymath2, и в более позднем посте была предложена следующая проблема.

Гипотеза: Для любого положительного целого числа существует такое, что если есть какое-либо подмножество плотности не менее, то содержит комбинаторную строку, такую ​​что набор подстановочных знаков имеет форму для некоторого подмножества.

Насколько мне известно, эта гипотеза остается открытой.

Оба вопроса «какие запрещенные закономерности в силе экспоненциально малой плотности» и «какие запрещенные закономерности в силе исчезающей плотности» интересны. Позвольте мне еще раз порекомендовать теорему Франкла-Родля и ее доказательство в качестве образца для подражания.

3. Четыре комбинаторные задачи в стиле Эрдёша.

3а. Задача Эрдёша о несоответствии

Это была задача, которая в итоге была выбрана для эрудит5 . Это была очень милая история. Проблема была представлена ​​в этом сообщении в блоге и выбрана как polymath5 после некоторых опросов среди читателей. Проект Polymath был самым продолжительным в истории Polymath. Было шесть предварительных постов для обсуждения с более чем 600 комментариями, за которыми последовал 21 официальный пост EDP1-EDP21. Было небольшое возрождение проекта (EDP22-EDP27) в 2012 году, когда я написал три поста. Известно, что в 2015 году Терри Тао решил эту проблему. Статья появилась в журнале Discrete Analysis. Решение Тао основано на некоторых выводах из проекта эрудита, включая важное сокращение, которое внес сам Терри. Он также в решающей степени опирался на (тогда) новую теорию Кайсы Матомаки и Максима Радзивилла. Решение было вызвано комментарием в блоге Уве Строински, который указал на возможную связь с EDP, и последующим комментарием Кодлу, который поддержал предложение Уве. Об этом сообщается в EDP28, и здесь, в моем блоге, мы отметили решение в этом посте.

3б. Гипотеза Эрдеша-Хайнала.

Позвольте быть положительным целым числом и пусть быть графиком. Эрдёш и Хайнал предположили, что существует константа такая, что если есть любой граф, по крайней мере, с вершинами, который не содержит индуцированной копии , то либо , либо содержат клику размера .

Тим утверждал, что самый простой открытый корпус — это пятиугольник. Этот особый случай был недавно разрешен Марией Чудновски, Алексом Скоттом, Полом Сеймуром и Софи Спиркл. Они полагаются на недавние результаты Яноша Паха и Иштвана Томона. Посмотрите эту видеозапись лекции Пола Сеймура из IBS Discrete Mathematics Group, Южная Корея.

3с. Гипотеза Франкла о замкнутом союзе.

Позвольте быть набором наборов, который замкнут относительно объединения. Должен ли существовать элемент, который содержится хотя бы в половине множеств?

Тим написал: Это печально известный вопрос, и, возможно, наименее подходящий для полиматического подхода (такое ощущение, что может возникнуть всплеск идей, ни одна из которых не сработает, за которым последует разочарование, или же, если нам очень повезло, единственная блестящая идея от одного человека, которая по сути решила проблему, но я могу ошибаться).

Polymath21 в блоге Тима Гауэрса (запущен в январе 2016 г.) был посвящен гипотезе Франкла. Проблема все еще открыта.

3д. Проблема дельта-систем.

Этот вопрос адресован Эрдёшу и Радо. Дельта-система  – это набор наборов  , такой, что все наборы  (с ) равны. Эквивалентно, существует некоторое множество такое, что для каждого и множества не пересекаются.

Эрдёш предложил 1000 долларов за решение следующей задачи: существует ли константа такая, что для каждой системы, состоящей как минимум из наборов размеров, должны существовать три из них, образующие дельта-систему?

Я посвятил polymath20 этой задаче. Я пытался продвигать некий гомологический подход. Это не привело к прогрессу, но привело к некоторым интересным наблюдениям по проблеме, а также к некоторому уточнению и лучшему пониманию моего подхода.

Несмотря на то, что проблема все еще открыта с 2009 года, в отношении проблемы, которую мы описали здесь и здесь, произошли серьезные прорывы, в первую очередь проблема была почти решена Райаном Алвейсом, Шачаром Ловеттом, Кевеном Ву и Цзяпэном Чжаном.

4. Нематематические проекты.

4а. Разработка нового типа шахматной программы.

Точная формулировка была такой: «насколько хороша программа для игры в шахматы, если объем доступной памяти очень ограничен, а объем вычислений также ограничен?» В комментарии Тим объяснил, что хотелось бы найти метод программирования, применимый ко всем играм определенного типа (таким как Отелло, Го и т. д.), а не только к шахматам. И это можно было бы принять за цель.

В одном комментарии упоминались новейшие на тот момент компьютерные программы для игры в го (основанные на машинном обучении). Позвольте мне упомянуть, что глубокое обучение привело к революции в этой области примерно в 2015 году. Происхождение жизни.

Это довольно предварительное предположение заключалось в том, чтобы попытаться создать модель, которая убедительно показала бы, как жизнь может возникнуть из неживого чисто натуралистическими процессами. Это обсуждалось далее в этом посте. Вокруг этого было много ажиотажа, но это не привело к полиматическому проекту, и я не уверен в прогрессе после 2009 года. .

В качестве отступления позвольте мне упомянуть, что Обри де Грей, который лихо улучшил нижнюю границу хроматического числа плоскости (что привело к полимату26), очень известен своими работами и идеями о старении. Я предложил Обри, чтобы у него был проект в стиле эрудита по проблеме старения и его подходу к этой проблеме. Однако Обри ответил, что различные попытки сделать что-то подобное на протяжении многих лет терпели неудачу во многих областях биологии.

5. Предварительный подход к нижней границе сложности.

Это превратилось в серию постов (первый здесь, вся «категория сложности» здесь), где Тим пытался развить несколько идей, связанных с проблемой.

________

Хорошо, теперь позвольте мне кратко и предварительно высказать некоторые предложения для моего будущего полиматического проекта.

Возможные будущие проекты Polymath (2021 г.)  

1. Гипотеза 3ᵈ и гипотеза флага для центрально-симметричных многогранников .

2. Математические вопросы о функциях социального обеспечения. Вот связанный пост 2009 года и опрос Эльханана Моссела.

3. Разработка теории в стиле эрудита

Может ли проект эрудита использоваться для разработки теории, а не для решения проблемы? Этот вопрос был поднят Питером Сарнаком в ходе дебатов IAS 2010 года о проектах эрудита.

3.a Теория выпуклых оболочек вещественных алгебраических многообразий . Один проект в этом духе, который я уже предлагал, состоит в том, чтобы попытаться полиматематическо разработать теорию выпуклых оболочек вещественных алгебраических многообразий.

3.b Распространение алгебраического сдвига на широкий спектр комбинаторных структур. Это проект с Элен Барсело середины 90-х, который в то время так и не был реализован, и было бы очень приятно исследовать его вместе.

Какие еще теории вы хотели бы, чтобы они развивались открыто и коллективно?*

4. Касание непересекающихся симплексов – 2ᵈ-гипотеза.

5.   Комбинаторные задачи Эрдёша. Две возможности:

5.a Гипотеза Симони; и 5.b Гипотеза Чватала .

Оба можно найти в конце этого поста. Дополнительные ссылки, SC1, SC2, CC1, CC2

6. Перечисление – веса на помощь (извините за расплывчатость)

7. Компьютерная математика (пока что это еще более расплывчато; но см. этот вопрос МО; здесь я думаю об экспериментальном проекте. Большинство других проектов могут включать в себя большие компоненты компьютерных экспериментов.)

8. Существует ли статистическая методология для выявления предвзятого выбора данных и связанных с ними статистических глупостей.    См. этот пост и слайды Майи Бар Гилель, а также этот пост Омера Рейнгольда о Windows в теории.

9. Проблема, поставленная Одедом Шраммом: Существует ли такое, что для каждого существует набор постоянной ширины 1 в размерности, объем которого удовлетворяет . (объем -мерного шара ширины один.) См. этот вопрос МО.

Мета-вопросы

Существует множество мета-вопросов, касающихся полиматологических проектов: 

1. Один из важных вопросов: какая платформа идеальна для полиматического проекта?
2. Может ли компьютер модерировать проект эрудита?
3.  Каков потенциал проектов эрудитов? Ограничения? Являются ли эрудитные проекты хорошим способом заниматься математикой.
4. Каковы стимулы для участия?
5. Являются ли эрудитные проекты привлекательными с точки зрения разнообразия участников?

* Интересно, может ли вопрос «Какую математическую теорию вы хотели бы увидеть в разработке» на Math Overflow останется в силе и приведет ли он к хорошим ответам. (Был хороший вопрос о том, какую книгу вы хотели бы видеть написанной. )

 

 

Нравится:

Нравится Загрузка…

Эта запись была размещена в Комбинаторика, Математика в Интернете, Открытое обсуждение и помеченный эрудит, Предложения Polymath, Тим Гауэрс. Добавьте постоянную ссылку в закладки.

Этот причудливо-гениальный шеф-энциклопедист меняет будущее еды

Соус из ферментированной белки в первом блюде Noma за 500 долларов в меню дичи и леса прошлой осенью не был на вкус таким пушистым-лесным-грызуном-вперёд, как вы могли бы ожидать. Добавляемый по капле в своего рода суп, он был скорее пикантной фоновой приправой, чем чем-то, что вы могли бы узнать без предупреждения — немного похоже на высококачественную, очень естественную миссис Дэш. В Noma, копенгагенском заведении, который многие считают лучшим рестораном в мире, персонал подает блюда просто, избегая терминов внутренней кухни и длинных списков ингредиентов, какими бы необычными ни были некоторые из этих ингредиентов. Таким образом, краткое изложение этого супа на нашем сервере было кратким и, учитывая его компоненты, не совсем информативным. Он использовал описание «теплый грибной чай».

Но мой партнер по обеду Дэвид Зильбер знал все секреты кухни. Спокойный, в черной водолазке, в очках 1980-х годов и косах с пробором посередине, Зильбер имеет одну из самых экзотических должностей в профессиональной кулинарии: он директор Noma по ферментации. Таким образом, он является одной из ключевых творческих сил в ресторане со своей собственной лабораторией и командой исследований и разработок, а также с растущим международным сообществом. В то время как другие кухни могут просто покупать ингредиенты или добывать их, если они амбициозны, повара Noma полагаются на Зильбера и его команду, чтобы изобретать многие из наиболее важных элементов своих блюд, как правило (но не всегда) с помощью магии микробиологии. Некоторые из самых гордых творений Зильбера включают мисо на основе бананового хлеба; нечеткие блинчики на основе плесени, которыми можно обернуть мороженое; и «экстракт петрикора», причудливый термин для бутылочного запаха горячего летнего дождя. Не говоря уже о соусе из ферментированной белки. В кулинарном мире он эквивалент Q. 9 Джеймса Бонда.0003

Как причудливо-блестящий местный эрудит Номы, он шеф-повар, который бросается такими терминами, как телос и Gesamtkunstwerk в непринужденной беседе, который читает квантовую механику, чтобы расслабиться. Его татуировки включают тессеракт, уравнения Шредингера и Максвелла и карту Млечного Пути. Он может — и его часто просят — на лету разложить таксономию ягод облепихи или североатлантических ежей.

И он совсем не похож на обычного кухонного работника. Зильбер — парень в толстовке с шипами в виде тетраэдра и дизайнерских штанах Hammer. (Как выразился его школьный друг: «В основном он одевается так, будто собирается в открытый космос».) Время от времени он подрабатывает фотомоделью, а также арт-фотографом; несколько его изображений находятся в постоянной коллекции Foam Fotografiemuseum в Амстердаме. Следует подчеркнуть, что это не обычные привычки и увлечения тех, кто трудится на кухнях мишленовских ресторанов. Так что, возможно, неудивительно, что его имя становится известным.

Только за последние шесть месяцев Зильбера по-разному называли «Гением брожения Номы» ( Vice ) и «Одним из самых новаторских деятелей в мире продуктов питания» ( Нью-Йорк журнал), а в ресторане его прозвища включают «Ходячую Википедию» и «Зильбертрон». Рене Редзепи, шеф-повар и совладелец Noma, часто представляет Зильбера как «второго по известности чернокожего еврея из Торонто». Шеф-повар и совладелец

Noma Рене Редзепи, который часто представляет Зильбера как «второго по известности чернокожего еврея из Торонто», объединился со своим парнем по ферментации, чтобы написать кулинарный бестселлер, выпущенный прошлой осенью

В октябре прошлого года Redzepi и Zilber выпустили The Noma Guide to Fermentation, удивительно удобочитаемую 500-страничную квази-поваренную книгу по уходу и подкормке различных плесеней, дрожжей и некоторых наиболее вкусных видов бактерий. К ноябрю книга вошла в список бестселлеров New York Times . Случайные читатели обычно отмечают Зильбера в Instagram, чтобы показать странный уксус и чайный гриб, которые они варят, или хурму, которую они уговорили подвергнуть лактоферментации на своих кухонных островах. Путеводитель был одной из самых актуальных книг осени.

Первое блюдо в тот вечер в ресторане, этот грибной чай с белкой, был столь же уместным показом, как и любое изумительное изящество, которое льется из разума Зильбера. Чаши были наполнены грудами мха и темно-зеленых сосновых побегов. Сосновая шишка была полузакопана в подлеске каждой чаши, как будто она попала во время бури. Струйки пара поднимались сквозь мох, как утренний туман. И все же все это было так же естественно, как швейцарские часы.

Мох, как сказал мне Зильбер, был сбрызнут этаноловой взвесью, которую повара Номы называют «экстрактом лесной подстилки». Он взбивает его в своем экстракторе сверхкритической жидкости, оборудовании стоимостью 100 000 долларов, предоставленном взаймы его поклонником из фармацевтической промышленности. Он отправляет своих собирателей после дождя за мхом, землей, корой, ветками и листьями. Затем Zilber обезвоживает и измельчает все это перед тем, как отправить в машину. За полный рабочий день машина выплевывает один сверхконцентрированный флакон. Чтобы добавить немного привлекательности бульону под мхом, его лаборатория произвела вещество, называемое лактоборовой водой: шипучий, острый грибной сок с диким электрическим вкусом, который образуется при добавлении свежих белых грибов, соли и молочнокислых бактерий тусуются вместе в банке.

Эффект белки также нельзя было отрицать. Его происхождение восходит к нескольким годам, когда ферментационная лаборатория Noma начала возиться с приготовлением рыбного соуса. Они пробовали кальмаров, устриц, сельдь и собранных в дикой природе моллюсков, обильно солили их перед тем, как запечатать в банки и оставить, чтобы морепродукты медленно гнить. Длительное, медленное расщепление белка производит многие из тех же нот, которые вы получаете в жареном мясе, а также большое количество полностью натурального глутамата натрия. Между тем соль не дает всему этому зайти слишком далеко. Эта техника восходит к карфагенянам, если не раньше — римляне называли эти соусы гарумами — и более или менее так рыбный соус в Юго-Восточной Азии делают до сих пор. Вскоре лаборатория начала заниматься не только рыбой и морепродуктами, но и разлагать такие наземные белки, как личинки восковой моли и бедро северного оленя. И их величайшее новшество заключалось в том, что они обнаружили, что, добавив немного aspergillus oryzae (это тот же ингредиент, что и соевый соус и мисо), вы получаете все характеристики жареного мяса и натуральный, усиливающий вкус глутамат натрия, с гораздо менее гнилостным запахом.

Это понимание изменило то, как повара Noma выполняют одну из самых фундаментальных задач в кулинарии: приправляют пищу. «Гарумы… не играют главной роли, но они там, под поверхностью, наполняя блюда нематериальной магией, фокусируя и оживляя естественные ароматы», — пишет Зильбер в Руководство Noma по ферментации. Другими словами, зачем добавлять соль в суп из свежих моллюсков, если можно добавить креветки и гарум из шиповника? Почему бы вам не добавить в свой теплый грибной бульон немного беличьей гнили, привитой плесенью?

Вот этот бульон из беличьих шампиньонов. Мох опрыскивают веществом, которое Нома называет «экстрактом лесной подстилки», взбитым в экстракторе сверхкритической жидкости стоимостью 100 000 долларов

. В любом случае, когда прибыли эти миски, мы с Зильбером оба сунули в них свои носы. На пару секунд я закрыл глаза и вдохнул его. Сила этой миски, мха, лесного концентрата и беличьего сока, этого неосязаемого волшебного дымящегося грибного супа была мгновенной; пахло эльфийским пикником в лесистой лощине, вполне возможно, под воздействием ЛСД.

Зильбер поднес чашу к лицу и сделал глоток. «Это чертовски вкусный бульон», — сказал он.

Если бы вы набросали персонажа, соответствующего фразе «самое воспитанное в Торонто когда-либо», результатом мог бы стать Дэвид Зильбер. Его мать, Ивонн Боуэн, родилась на Кюрасао и эмигрировала в Канаду в возрасте 20 лет, поселившись в подвальной квартире трехэтажного дома в Монреале. Молодой управляющий зданием Гарри Зильбер жил наверху. Он проявлял интерес, выходящий за рамки чисто профессиональных потребностей. Супруги переехали в Торонто, и в 19 лет родился Давид Хаим Джейкоб Зильбер.85. Годы спустя, как единственный темнокожий ребенок в туристическом автобусе, полном подростков в Израиле, он получил награду за самое еврейское имя.

Зильберы жили в Дон-Миллс, в квартире с двумя спальнями за комплексом Арахисовая Плаза, где и по сей день можно купить свежий ямайский кокосовый хлеб, персидскую смесь орехов, а также региональные китайские и тамильские блюда на вынос, а затем подавать все это осенью. — Кроме предметов домашнего обихода из Долларамы несколькими дверями вниз. Такое смешение, которое другие люди могли бы назвать гипермультикультурализмом, не было чем-то особенным для Зильбера. В то время он не считал это преимуществом, не считал такую ​​среду, которая могла бы способствовать адаптации и открытости новому опыту — которая могла бы дать толчок будущему шеф-повару. «Это лучшая часть Торонто — все люди разные. Ты приходил к кому-нибудь домой и каждый вечер ел что-то новое», — говорит он.

Домашняя жизнь Зильбера, в Дон Миллс, а затем в Скарборо, была почти такой же разнообразной. «Столкновение двух культур, — говорит он. Ивонн обратилась в иудаизм, и ее свекровь Зофия научила ее готовить суп с шариками из мацы, латкес и фаршированную рыбу. По пятницам семья ела традиционный ашкеназский еврейский шаббатный ужин. Потом по субботам лакомились соленой рыбой и пекли. Зильбер, которого часто можно было встретить на кухне рядом с матерью, научился жарить латке и бананы, а также карамелизовать настоящий плов.

У него также появилась фиксация на приправе с глутаматом натрия, которую его мать держала под рукой. «Я всегда тянулась к желтой бутылке, клала ее в руки и просто облизывала ее, как олень солонка, каждый вечер, когда моя мама готовила ужин. Это было похоже на крэк-кокаин», — говорит он. «Теперь вся моя гребаная работа состоит в том, чтобы делать все это. Полный круг, я думаю.

Ивонн, дошкольный воспитатель для детей с особыми потребностями, была прирожденным воспитателем. Она дала своему сыну терпение, индивидуальность и утешение в том, кем он был. Даже на том этапе жизни, когда многие дети не хотят ничего, кроме как быть анонимными, Зильбер упивался тем, что он одновременно черный и еврей — будучи, как выразился один из его давних друзей, «двойным меньшинством». Он научился уживаться где угодно. «Если я общителен, общителен или обаятелен, я определенно получаю это от нее», — говорит он. «И если я занудный и склонный к технологиям, я определенно унаследовал это от своего отца». Гарри, авиационный инженер, работал в компании De Havilland недалеко от аэропорта Даунсвью.

Зильбер мечтал заниматься наукой. Его любимыми книгами были 20-томная серия Time-Life «Путешествие по Вселенной». Он расположил светящиеся в темноте звезды в созвездия на потолке своей спальни и с помощью своей матери сделал свой собственный костюм Энакина Скайуокера, чтобы надеть его на Атака клонов. Зильбер также носил корсет для спины — жесткий корсет из стекловолокна — для лечения сколиоза. Он и его школьные друзья притворялись, что скоба — это неразрушимый щит. В их подростковом воображении Дэвид был супергероем по имени Нерушимый.

Подпишитесь на нашу рассылку Спасибо за регистрацию!

Чтобы быть в курсе последних новостей о Торонто, подпишитесь на This City Теперь проверьте свой почтовый ящик, чтобы завершить подписку

И все же Зильбер, который провел 12 лет погружения во французский язык, не совсем соответствует требованиям ботаника. Несмотря на его любовь к космосу и астрономии, его оценки были не очень хорошими. Зубрежка средней школы редко имела для него смысл. Ему нужно повествование и связи, чтобы понимать вещи — он не может делать детализацию. В конце года обучения в York Mills Collegiate Зильбер наблюдал, как его друзья поступают в U of T и Ryerson. Он хотел стать палеонтологом. «Глядя на свои оценки, я думал: «Я никуда не пойду», — говорит он.

Сочувствующий консультант вспомнил о его интересе к еде и кулинарии и направил его на программу ученичества. Он прошел три недели элементарного обучения кухне, а затем приземлился в новом ресторане под названием «Рейн» на Мерсер-стрит. С самого начала Дэвид Зильбер не был похож на других поваров.

В холле Rain был водопад, а в списке коктейлей — сакетини. Это было суетливо и дорого, но с современной атмосферой. Станция garde manger ежедневно производила 128 гарниров, таких как усики гороха, завернутые в побеги попкорна, и крошечные корзиночки из корней таро, обжаренных во фритюре. Такая степень «драгоценной, яркой гастрономической безрассудности», как назвал ее один рецензент, была бы невозможна без низкооплачиваемой помощи на кухне.

Зильбер, которому было 18 лет, когда он начал, постоянно задавал вопросы. «Большинство поваров в этом возрасте просто питаются адреналином от загруженного обслуживания… все это сумасшествие с гормонами адреналина», — говорит Гай Рубино, шеф-повар, совладелец заведения. — А он никогда таким не был. Зильбер должен был знать, почему и как: что заставляет вкусы и процессы работать.

И говорил он странно хорошо. В свободное время он читал художественную литературу. В выходные дни он часто посещал художественные открытия и галереи и снимался в видеороликах, снятых его друзьями-кинематографистами, сам ставя хореографию и оформляя их. В то время современники Зильбера часто недоумевали, почему он хлопочет поваром. Тем не менее, он рос, чтобы любить свой новый выбор карьеры. Он оказался в окружении самых энергичных молодых поваров города, и их энтузиазм был заразителен. Кроме того, вы могли бы попробовать что-нибудь на этой кухне, придумать что-нибудь на ходу. Никто не должен был говорить клиентам, что подросток, который никогда не прикасался к рису для суши до нескольких месяцев назад, был оставлен ответственным за их курс нигири за 35 долларов за шесть укусов.

Шеф-повар из Ванкувера по имени Дэвид Хоксворт пригласил Зилбера в свой ресторан West. В то время как архетипическим линейным поваром той эпохи был жадный до виски, шлепающий по заднице и трудолюбивый кухонный ковбой Энтони Бурдена, Зильбер был тощим книжным эстетом. В первые дни на «Уэсте» чрезмерное размышление Зильбера сделало его склонным к ошибкам. «Я знал, что он чрезвычайно умен, — вспоминает Хоксворт. «И что он, вероятно, мог бы использовать свой интеллект по-другому, в гораздо менее агрессивной среде». В течение следующих нескольких лет он провел время в «Колборн-лейн» Клаудио Априле, затем в «Здоровом мяснике», где дослужился до заместителя командира.

В начале 2011 года у Зилбера была еще одна встреча с Дэвидом Хоксвортом, который набирал ключевой кухонный персонал для одноименного нового ресторана без лишних усилий в ванкуверском отеле Rosewood. Наконец, все уроки, которые Зильбер усвоил, — все вопросы, которые он задавал, и все его размышления — начали приносить свои плоды. Его мировоззрение значительно повзрослело со времени его пребывания на Уэсте; он понял, что его опыт под руководством Хоксворта сделал его лучшим поваром.

Зильбер работал в Рейн, Уэст и Колборн-лейн, среди прочего, прежде чем приземлиться в Нома 9.0002 Зильбер изменился и в другом. Во-первых, его привычки к чтению расширились далеко за пределы художественной литературы. Он начал зачитываться лингвистикой и социологией, астрофизикой и международной экономикой — тем, что можно назвать только «Большими важными книгами». Он читал Джеймса Глейка и Стивена Хокинга, книгу Томаса Куна «Структура научных революций » и книгу лингвиста Гая Дойчера «Через стекло языка». Его разум был взорван Ричардом Докинзом Эгоистичный ген и «» Дэвида Дойча «Начало бесконечности». Когда я послал ему по электронной почте список, он ответил фразой, которую часто приписывают Эмерсону: «Я не могу вспомнить книги, которые я читал, так же, как и блюда, которые я ел, но в любом случае они сделали меня. ” И все же он помнил, что читал — обычно все.

Зильбера наняли в Хоксворт не линейным поваром, а су-шефом. Он начал развивать кулинарный стиль. Его покрытие было далеко за пределами Ванкувера, что было нормальным для того времени. Он украшал свои блюда съедобной почвой и золой кинзы. Он играл с негативным пространством, устраивая свою еду вокруг края тарелки, оставляя ее центр пустым. «Это была его личность на тарелке», — говорит Кристиан Эли, шеф-повар ресторана.

И Зильбер умел использовать другие свои таланты. Когда что-то из кухонного оборудования, блендера или су-вид машины, вышло из строя, он кинул его в рюкзак и забрал домой. Поздно ночью он отвинчивал болты и разбирал машину по частям. Часто, ради прикола, он отправлял Элаи фото разрушений посреди ночи: 60 или 70 деталей машин, разбросанных по полу его спальни. На следующее утро Зильбер доставал машину из рюкзака, и она работала как новая. «В Хоксворте я годами не платил за техническое обслуживание мелкого оборудования, — говорит Эли.

В те годы список 50 лучших ресторанов мира набирал силу. Идеи, которые вы когда-то должны были увидеть, теперь распространяются через Instagram за микросекунды. Зильбер хотел учиться на лучших кухнях Земли. Поэтому осенью 2013 года Хоксворт написал ему восторженное рекомендательное письмо. («Я с большой гордостью могу порекомендовать вашему заведению моего су-шефа и давнего протеже Дэвида Зильбера».) Зильбер составил сопроводительное письмо, озаглавив его вверху жирным шрифтом: Сопроводительное письмо.»

«Я тот, кто сидит на кухне во время обеда для персонала, объясняя, как микроволновое излучение нагревает воду, или антропологические и эволюционные доводы в пользу того, почему выращенная на ферме клубника на вкус отличается от дикой», — написал он.

«Я попросил пару своих поваров прочитать его», — говорит Зильбер. «Мы все собрались выпить. Я такой: «Эй, ребята, что вы об этом думаете?» А они такие: «Не рассылайте это; ты звучишь как сумасшедший».

Он все равно отправил его Алинее в Чикаго, Сезону в Сан-Франциско и Номе. «Первые два вроде абсолютно молчат. А потом Нома вернулся ко мне в течение двух недель». Зильбер вылетел в Копенгаген на короткое испытание, и его нанял шеф-повар Дэн Джусти. Большую часть следующего года Зильбер редко спал.

Нома немного напоминает летний лагерь на берегу озера, переосмысленный скандинавским архитектором. Комплекс представляет собой группу из 11 зданий, большинство из которых соединены проходами из бетона, дуба и стекла. Снаружи есть три теплицы и дощатый настил, который ведет через продуваемую ветром прерию с высокой травой. Это первое место, где я когда-либо ел, где вы можете наблюдать, как дикие утки плавают и гнездятся прямо за окнами, жуя своих кузенов по другую сторону стекла.

Комплекс «Нома» представляет собой кластер из 11 зданий, соединенных переходами из бетона, дуба и стекла. Это немного похоже на летний лагерь на берегу озера, переосмысленный скандинавским звездным архитектором

Когда Зильбер прибыл сюда весной 2014 года, он обнаружил кухню, заполненную кричащими, ругающимися, часто охваченными паникой поварами. Noma впервые появился в списке 50 лучших ресторанов мира в 2007 году под номером 15. В следующем году он занял 10-е место, а к 2010 году поднялся на первое место. Кухонная бригада Номы должна была делать невозможное с каждой тарелкой.

В первый год Зильбер работал поваром в холодном отделе ресторана — «самая дерьмовая работа в Noma», как он ее называет. Он отвечал за ежедневное производство 400 листов равиоли из листьев черемши, разновидности лука-порея; ему приходилось нарезать 300 идеальных квадратов из жареной свеклы каждое утро к обеду Номы, а затем повторять процесс для ужина позже в тот же день. Он делал бульоны и соусы. Он готовил, отдыхал и делил тыквы на порции. Несколько дней ему помогала пара из stagiaires, , в то время как в другие дни он этого не делал. Он редко знал заранее. Ожидалось, что он также будет работать на каждой службе, готовя на очереди обед и ужин. В большинстве случаев он уходил на работу в 5:30 утра, задолго до восхода солнца, приходил домой после часа ночи следующего дня, затем просыпался через три или четыре часа и делал все заново.

Мало у кого из коллег Зильбера было время на любезности, не говоря уже о том, чтобы нянчиться с новым сотрудником. Когда подготовка Зильбера задерживалась, что случалось часто, повара кричали на него. Не имело значения, были ли его стажеры переназначены на этот день или если ему, не по его вине, поручили работу пяти поваров.

Хуже того, в рецептах Номы — одних из самых сложных и оригинальных блюд — перечислялись лишь меры и ингредиенты. Что касается метода, то повара должны были либо интуитивно знать, либо каким-то образом понять его. «Нет оправдания. Никогда не было оправдания. У вас не должно быть оправданий», — говорит Зильбер. (Кухня, по общему мнению, в последние годы стала гораздо менее жестокой.)

Чем Зильбер действительно выделялся, так это своей способностью общаться, особенно с гостями ресторана. Его сообразительность и добродушный юмор — его способность ладить — сделали его популярным во время кухонных экскурсий. Он понял общую картину того, как работает ресторан, и характер его миссии. И пригодились его 12 лет французского погружения. «У нас были известные французские повара, которые не говорили по-английски, и они немного скептически относились к Noma, ко всей этой скандинавской кухне», — говорит Дэн Джусти. «Это было большое давление на ресторан. Мы всегда давали эти туры Дэвиду».

Еще одно преимущество: на кухне Номы никогда не было ничего постоянного. В начале 2015 года весь персонал переехал в Токио на два месяца, и кухня была перетасована. Рабочая нагрузка Зильбера превратилась из невозможной в просто смешную, а затем в ту же, что и у других поваров. После ежедневного ада, который пережил Зильбер, Noma Japan была проще простого.

Если у Зильбера и было какое-то другое качество, способствующее карьерному росту, так это его готовность бросить вызов: его чистая, необузданная смелость. Он был счастлив быть аутсайдером, если вообще когда-либо задумывался о своем месте в жизни. Раз в неделю выбирался шеф-повар, который представлял собственное блюдо всему персоналу. Эти презентации, получившие название «Проекты субботним вечером», были крайне напряженными для поваров Noma. Некоторые из них были пусты, говорит Джусти, не в состоянии говорить. Зильбер, с другой стороны, никогда не казался нервным. Это был персонал, который часто терял дар речи к тому времени, когда он заканчивал. Однажды Зильбер преподнес огромную тарелку пасты, но из нее удалили лапшу, чтобы он мог подавать только оставшийся соус. Другой его проект назывался «Размышления о солипсизме на побережье Средиземного моря (9).1096 De Gustibus Non Est Disputandum ) Вариации 1–4».

Когда они вернулись в Данию, Джусти назначил Зильбера ответственным за барбекю в ресторане. Эта работа была важным шагом вперед. «Там много умных людей, — говорит Джусти. «Но Дэйв не беспокоится о неудаче. Он не беспокоится о том, что кто-то подумает о нем, и именно это позволяет ему добиться того, чего он достиг».

В начале 2009 года Редзепи и пара его лучших поваров пришвартовали деревянный плавучий дом в гавани Копенгагена, напротив ресторана. Это было экспериментальное пространство с открытым исходным кодом для разработки новых идей и ингредиентов. Хотя брожение было лишь частью того, что изучали шеф-повара лаборатории, Редзепи сразу же увидел отдачу. Один из поваров запечатал свежие ягоды крыжовника в вакуумный пакет с небольшим количеством соли, чтобы поощрить бактерии, которые будут использовать ферменты для расщепления сахаров, производя новые ароматные метаболиты. «Я попробовал его и был совершенно потрясен», — сказал Редзепи. Ферментация, как он понял, может значительно расширить кладовую Noma, ориентированную на местное население, раскрывая новые текстуры и вкусы основных скандинавских продуктов.

Зильбер и его команда создают многие ингредиенты для кухни с нуля, например, кожуру фруктов, отлитую в виде жука. в резиденции, химик по имени Ариэль Джонсон. «Люди всегда тесно ассоциировали наш ресторан с дикой едой и поиском пищи, — пишет Редзепи в Noma Guide, , — но правда в том, что определяющим столпом Noma является ферментация».

Очередь Зильбера настала в 2015 году, когда Уильямс и Джонсон решили двигаться дальше. «Работа с самого первого дня должна была быть чрезвычайно напряженной, — говорит Джусти. «Весь ресторан опирался на эту ферментационную кухню в поисках вдохновения, ингредиентов и производства. Они создавали множество продуктов, которые использовались во всем меню. Эти вещи нужно планировать заранее».

До этого Зильбер никогда особо не задумывался о ферментации. Если не считать того, что десятью годами раньше он приготовил немного кимчи в ресторане Rain, он тоже почти ничего не сделал. Но Зильбер, чей жизненный девиз — «оставайся любопытным», умел учиться.

Когда однажды в декабре я прибыл в лабораторию, заместитель Зильбера, бывший внештатный консультант по ферментации по имени Джейсон Уайт, готовил и процеживал пробные партии люпина, органической бобовой культуры, выращенной в Швеции, с прицелом на превращение богатое белком молоко бобовых в веганский йогурт. Лаборатория также находилась в постоянном производственном цикле для охотничьего и лесного меню Noma, смешивая, подготавливая и ферментируя десятки ингредиентов, доступных только в Noma, для ежедневного обслуживания. Хьюго Чейз, веселый 30-летний шеф-повар, процеживал соевый соус из копченых водорослей в 20-литровое ведро. Тем временем Зильбер проверял одно из своих самых трудоемких творений на тот момент — своего рода покрытые плесенью ячменные чипсы, которые были ключом к блюду под названием «лепешки с трюфелем».

Зильбер разработал способ выращивания плесневого грибка aspergillus oryzae на листах пропаренного прессованного ячменя толщиной в один миллиметр. Как он недавно описал полученный продукт: «У вас есть этот нечеткий, бархатистый белый ковер со вкусом жимолости и сладкого абрикоса. Но на языке такое ощущение, будто ты облизываешь замшевую сумку». Те листы, которые Зильбер вытаскивал из вращающейся стойки подносов, были лепешкой; Кухня Noma каждый день нарезала их по форме контурных перьев утки кряквы, а затем тщательно покрывала каждое из них кусочками черного трюфеля для почти идеальной (и смехотворно вкусной) trompe l’œil.

Лаборатория напомнила мне странного старомодного аптекаря, но с химическим оборудованием, которое можно увидеть в сериале «Во все тяжкие». По обеим сторонам помещения со столешницей из нержавеющей стали располагались проходные бродильные помещения, заполненные полками с булькающими, помеченными клейкой лентой банками, содержащими странно звучащие фруктовые соки, мисо, чайный гриб, гарум, соусы шою, уксусы и основные маринованные фрукты. Под прилавком, в задней части лаборатории, центрифуга типа тех, которые обычно используются в банках крови, крутила партию елового масла для тестовой кухни ресторана; рядом с ним высокий вращающийся испаритель все еще ярко светился зеленым светом из спиральной трубки антифриза в самой верхней его части. Там были канистры с жидким азотом и ультразвуковой гомогенизатор — он использует звуковые волны, по сути, для эмульгирования вещества. Несколько кувшинов с лабораторным этанолом стояли на полке для экстрактора сверхкритической жидкости Зильбера, который занимал большую часть длины одной стены. Зильбер и Уайт также ожидали поставки криогенного морозильника для хранения своих любимых бактерий при температуре -100°C.

Ферментационная лаборатория находится в постоянном производственном цикле, смешивая, подготавливая и ферментируя десятки ингредиентов, доступных только в Noma, для ежедневного обслуживания.

В нескольких шагах от Noma, в испытательной теплице, творческая группа ресторана завершала работу над весенним меню из морепродуктов. Каждый год Нома составляет три совершенно новых меню: овощи летом, дичь осенью, морепродукты с зимы до весны. Основная творческая группа, состоящая из Редзепи и шести старших поваров, работала над морепродуктами почти три месяца. Рыбный пирог и салат из мочевого пузыря трески, равиоли из морского салата и щечки мидий — только щечки, заметьте, — подавались в кастрюле с тем, что Зильбер называл «секретным бульоном». Дзюн Такахаши, шеф-повар из Японии, курсировал в теплице из якатори, которую он установил на подветренной стене, где он пытался понять, как жарить маринованные блоки из 9 штук.1096 aspergillus oryzae плесень для блюда из морского ежа.

Во всем этом Редзепи играет в основном роль креативного директора; он часто дает какие-то расплывчатые, но вдохновенные указания, а заполнение пробелов зависит от творчества. Блюда в основном уже были накрыты; за неделю до этого Зильбер провел дегустацию. Среди своих обязанностей Зильбер назначен дегустатором Noma, первым шеф-поваром, который съедает каждое меню от начала до конца. Когда его коллеги представили Зильберу дичь и лесное меню, одним из самых интересных блюд было целое крыло дикой утки с перьями, превращенное в своего рода леденец на палочке из утиного мяса, с жареной в темпуре барабанной дробью на конце. «Я подумал:« Это безумие за гранью; это полностью Noma!», — вспоминает Зильбер. «И Рене такой: «Но это лучше, чем жареный цыпленок?» «Абсолютно нет», — ответил Зильбер. Мясо было слишком жевательным для гостей. Его точка зрения была принята. На кухне крылышки разделывали по-другому, с кусочками грудки на концах вместо барабанных палочек.

В один из вторников, в 12:20, в сауне на территории Нома должен был состояться творческий процесс, который Редзепи называл медитацией — по-видимому, неотъемлемой частью творческого процесса Нома. Шеф-повар был непреклонен в том, что его творческая группа не должна это пропустить. Зильбер не двинулся к двери. Он воздерживается от сауны, сказал он. «Рене как-то спросил меня, почему я не присоединяюсь к ним: «Почему ты не идешь с нами, очисти свой разум?», — улыбается Зильбер. «Я сказал ему: «Потому что мне нравятся все голоса в моей голове». Редзепи хочет только лучших из лучших; вот почему Noma так знаменита. Ингредиенты здесь должны соответствовать как блюду, так и меню. В последнее время одним из любимых ингредиентов Зильбера является разработанное им чечевичное мисо. «Это потрясающе, — говорит он. «Это лучшее мисо, которое мы когда-либо готовили. Он чрезвычайно фруктовый и цветочный, с легкой ноткой черного перца». Он пока не может найти для него дом. Гарум из жареных куриных крылышек, приготовленный в ферментационной лаборатории, томился целых два года, пока не был представлен публике. Сегодня это один из самых популярных читов на кухне Noma. «Я могу развлекаться, пока коровы не вернутся домой, но в какой-то момент ты чувствуешь, что мужчине нужен телос: драйв, цель, цель», — говорит Зильбер. «Иногда в лаборатории ты такой: «О, посмотри, какую крутую штуку я сделал!» И все такие: «Вау, это интересно». И на этом все заканчивается».

Лаборатория Зильбера выглядит как старомодная аптека, но с оборудованием, которое вы можете увидеть в сериале «Во все тяжкие»

В конце этой зимы Зильберу предстоит операция по поводу сколиоза. Брекеты, которые он носил в подростковом возрасте, не помогли. За последние несколько лет он уменьшился на три сантиметра. Боль была изнурительной, и 15 лет на ногах на кухнях ресторанов не помогли. Хирурги планируют вживить ему в позвоночник стальной стержень, чтобы обходной путь вдоль позвонков превратился в прямой. «Похоже, это очень болезненно», — говорит он. По словам врачей, его восстановление должно занять около трех месяцев. Зильбер с нетерпением ждет выхода. «После того, как вы проработали в Noma пять лет, в вашей душе чувствуется усталость, — говорит он.

Он придумывал идеи для ресторанов еще со времен своей работы в Rain. Одной из первых его мыслей было открыть ресторан высокой кухни, который в нерабочее время трансформировался бы в столовую для бесплатного приема пищи. — Робин, — говорит он. «Его звали Робин. Мол, я бы взял у богатых и отдал бы бедным. И это была девичья фамилия моей бабушки по материнской линии. Ее звали Молли Робин.

«У меня также была идея ресторана под названием «Раб», который был бы похож на Noma, но с афроамериканской едой, и погрузился бы в антропологическую историю черной еды в Штатах и ​​Канаде», — говорит он.

Зильбер подумывал о том, чтобы организовать место для завтрака по соседству, как в «Спасительной благодати» Тринити Беллвуд, но на пятизвездочном уровне. И его самой сложной идеей был ресторан с дегустационным меню, который, как он описывает его, «использовал бы еду как средство для обсуждения философских идей». Однако на данный момент Зильбер все это выложил на обсуждение. Мысль об открытии собственного дома просто не работает. Успех сделал его будущее гораздо менее ясным. «Это был первый раз в моей жизни, после того как эта книга была выпущена, я подумал: «Я чувствую себя чертовски потерянным». Это очень странно».

Зильбер занялся кулинарией, потому что у него не было оценок, чтобы следовать своим мечтам, потому что он не чувствовал, что у него есть варианты получше. Теперь они у него есть. Когда вы являетесь одним из самых новаторских деятелей в мире продуктов питания, а также автором бестселлеров, то, как вы учились в старшей школе, больше не имеет особого значения.

В среднесрочной перспективе у Зильбера есть еще одна книга, которую нужно написать для Noma, сборник навыков и советов из ресторана, которые обычные читатели могут использовать дома. У него также есть на примете собственная книга: та, которая может показаться совершенно неуместной, если вы его не знаете. Это большой и важный рассказ о черных дырах и энтропии, солнечных системах, эволюции, капитализме и человеческом двигателе. «Распространяйте идеи через еду, кормите 100 человек за ночь», — говорит он. «Излагайте идеи в письменной форме и накормите 100 000 человек».

Каждый вечер Зильбер выступает с докладом перед сотрудниками Номы на такие несопоставимые темы, как выращенное в лаборатории мясо, свобода воли и утиные пенисы. Прошлой весной на открытии меню овощного сезона он рассказал о сельском хозяйстве, связав такие разрозненные явления и области, как человеческая эволюция и плодовитость, свобода воли, кузнечное дело, ловушка роскоши социологии и биотехнологии, в глубоко освещающее четырехминутное повествование. Для последнего игрового и лесного сезона он говорил на тему утиного секса. (Денежная линия: «Пенис аргентинской озерной утки на самом деле длиннее ее тела, и у многих уток член сравним с человеческим по длине».) Редзепи впервые попросил его провести переговоры в начале прошлого года в качестве своего рода упражнения по обогащению персонала. . Он называет их «Подкаст». Для запуска сезона морепродуктов в январе этого года Зилберт пошутил над эволюционной биологией китов.

Около 11 утра, как-то во время моего визита, Зильбер выбрал тему вечера: мясо, выращенное в лаборатории. Его лицо просияло, когда он это услышал. «Ах, клеточное сельское хозяйство!» Он выглядел как ребенок, которого попросили назвать его любимый вкус мороженого. Теперь, когда вокруг кухни Номы собралось около 80 поваров и обслуживающего персонала, он вытащил свой телефон и начал читать.

«Любите хороший стейк средней прожарки? Сочный бургер? Конечно, вы делаете!» он начал. Его речь ловко переплеталась от экологии к экономике, от веганства к здоровью человека, к генетической модификации микробов и капризам человеческого вкуса.